Condutores em Equilíbrio Eletrostático

Condutores em Equilíbrio Eletrostático

Campo e Potencial do Condutor

Um bom condutor possui elétrons livres. Se esses elétrons não apresentarem nenhum movimento ordenado, diremos que o condutor está em equilíbrio eletrostático. Para que isso ocorra, o campo elétrico no interior do condutor deve ser nulo pois se o campo fosse diferente de zero, provocaria movimento dos elétrons.

Na superfície do condutor pode haver campo elétrico não nulo, desde que ele seja perpendicular à superfície.

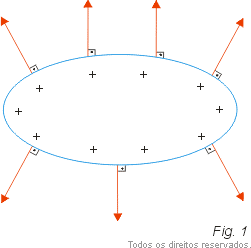
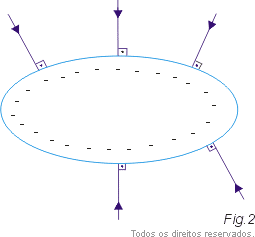
Por exemplo, se tivermos um condutor eletrizado positivamente (Fig. 1), na superfície o campo tem o sentido de afastamento e se o condutor for eletrizado negativamente, o campo é de aproximação (Fig. 2).

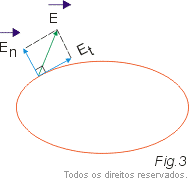
A necessidade de o campo ser perpendicular à superfície decorre do fato de o condutor estar em equilíbrio. Se o campo fosse inclinado em relação à superfície, como ilustra a figura 3, haveria uma componente tangencial que provocaria o movimento das cargas.

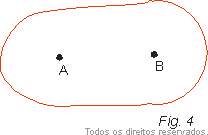
Consideremos agora dois pontos quaisquer A e B pertencentes a um condutor em equilíbrio eletrostático.

Se os potenciais de A e B fossem diferentes, haveria movimentação de elétrons livres do potencial mais baixo para o potencial mais alto o que contraria a hipótese de equilíbrio. Portanto concluímos que os pontos A e B devem ter o mesmo potencial:

Distribuição de Cargas

Quando um condutor está eletrizado, tem um excesso de cargas positivas ou negativas. Na situação de equilíbrio essas cargas tendem a se afastar o máximo possível e assim ficam na superfície do condutor. Se o condutor for esférico e isolado (longe da influência de outros condutores ) as cargas distribuem-se uniformemente pela superfície. (Fig. 5) Mas se o condutor tiver outra forma, as cargas concentram-se mais nas regiões mais pontudas.

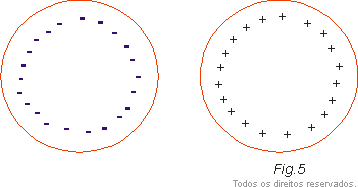
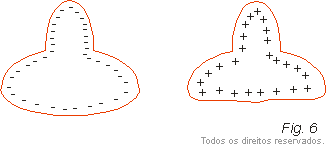
Para caracterizar essas diferenças define-se a densidade superficial de cargas. Se uma "pequena" superfície de área ΔA contiver uma carga Q, a densidade de cargas nessa superfície é definida por:

(I)

Assim, no caso do condutor esférico isolado, a densidade é constante ao longo da superfície. Porém para condutores de outras formas, a densidade é maior nas pontas.

Blindagem Eletrostática

Na figura 7 representamos um condutor neutro Y situado no interior de um condutor oco X. Independentemente do fato de X estar ou não eletrizado, o campo elétrico no seu interior é nulo. Desse modo, o condutor X protege o condutor Y de ações elétricas externas. Se aproximarmos, por exemplo, um condutor eletrizado A, (Fig. 8) este induzirá cargas em X mas não em Y. dizemos então que o condutor X é uma blindagem eletrostática para o condutor Y.

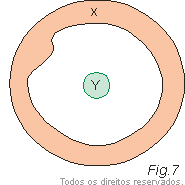
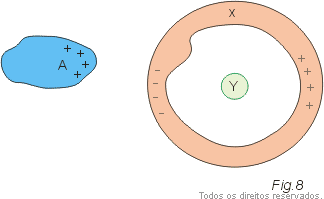
Essa blindagem é usada na proteção de aparelhos elétricos para que estes não sintam perturbações elétricas externas. A carcaça metálica de um automóvel ou avião e a estrutura metálica de um edifício também são exemplos de blindagens eletrostáticas.

Campo e Densidade

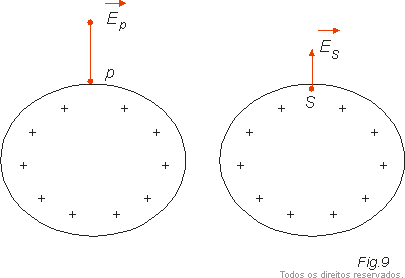
Consideremos um condutor em equilíbrio eletrostático. O campo elétrico em um ponto exterior P, "muito próximo" do condutor, tem intensidade dada por:

(II)

onde σ é a densidade superficial da cargas nas proximidades de P e E é uma constante denominada permissividade do meio. Essa constante está relacionada com a constante lei de Coulomb pela relação:

Assim, no vácuo, temos:

Em um ponto S da superfície do condutor, a intensidade do campo é a metade da intensidade no ponto P:

(III)

Das equações II e III percebemos que o campo é mais intenso onde a densidade de cargas for maior. Por outro lado, sabemos que a densidade é maior nas "pontas".

Portanto, o campo elétrico é mais intenso nas "pontas" de um condutor e esse fato é conhecido como poder das pontas.

Exemplo 1

Um condutor esférico de raio R = 2,0.10^-2m está eletrizado com carga Q = 7,5.10^-6C no vácuo. Determine:

a) a densidade superficial de carga

b) a intensidade do campo elétrico num ponto externo muito próximo do condutor

c) a intensidade do campo sobre o condutor

Resolução

a) supondo que o condutor esteja isolado as cargas distribuem-se uniformemente pela superfície. Lembrando que a área da superfície é temos:

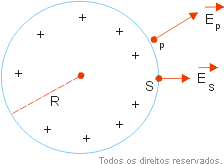
b) num ponto P externo é "muito próximo" do condutor, o campo tem intensidade dada por:

c) num ponto S da superfície, o campo tem intensidade igual à metade da intensidade no ponto próximo:

Condutor Esférico

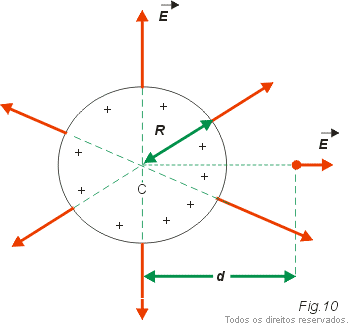
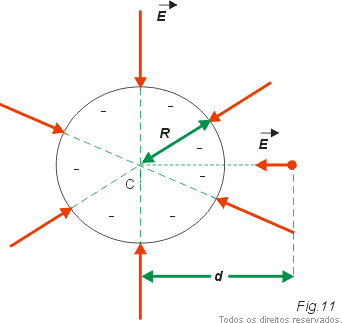
Consideremos um condutor esférico, eletrizado, em equilíbrio e isolado. Como já sabemos, o excesso de cargas distribui-se uniformemente pela sua superfície (Fig. 10 e Fig. 11).

No interior do condutor o campo elétrico é nulo. Porém no exterior o campo é não nulo e sua intensidade pode ser calculada como se toda a carga do condutor ( Q ) estivesse concentrada no centro da esfera, usando a equação válida para uma carga puntiforme:

(para d > r) ( IV)

Para calcular a intensidade num ponto "muito próximo", fazemos d = R:

(V)

É fácil verificar que esta equação dá o mesmo valor fornecido pela equação II:

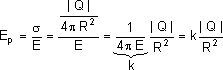
Na superfície o campo tem intensidade igual à metade da intensidade no ponto "muito próximo":

Desse modo o gráfico da intensidade do campo em função da distância d ao centro da esfera, tem o aspecto representado na figura 12.

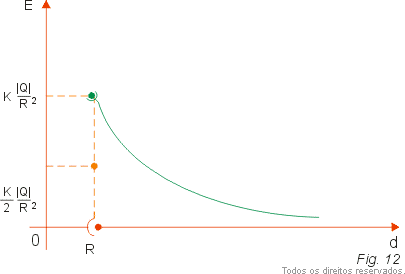
O potencial em pontos externos também pode ser calculado supondo toda a carga concentrada no centro e usando a equação da carga puntiforme:

(VI)

Na superfície do condutor, o potencial é obtido fazendo d = R:

(VII)

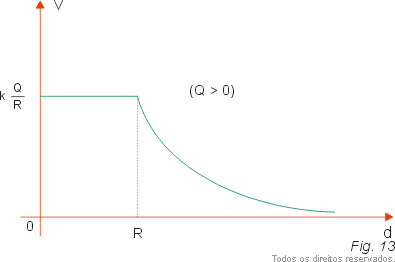
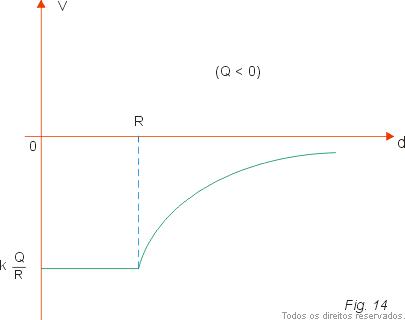
Como todos os pontos do condutor têm o mesmo potencial, a equação VII nos dá o potencial de todos os pontos do condutor. Assim, o gráfico do potencial em função da distância d ao centro da esfera tem o aspecto da figura 13 para Q > 0 e o da figura 14 para Q < 0.

Capacitância

Suponhamos que um condutor de formato qualquer esteja isolado. Se eletrizarmos esse condutor com uma carga Q ele terá um potencial V. É possível demonstrar que Q e V são proporcionais, isto é,

• dobrando a carga, dobra o potencial
• triplicando a carga, triplica o potencial
• etc.

Assim, podemos escrever

Q = C. V

ou

( VIII )

Onde C é uma constante de proporcionalidade chamada capacitância do condutor e que pende do meio e da geometria do condutor, isto é, do seu formato e tamanho. Como Q e V têm o mesmo sinal, a capacitância é sempre positiva.

No Sistema Internacional a unidade de capacitância é o farad ( F ):

Porém, em geral, as capacitâncias dos condutores com que trabalhamos são muito menores do que 1F; assim, usaremos submúltiplos:

Fórmulas

1m F = 1 mulifarad = 10^-3F

1 F = 1 microfarad = 10^-6F

1nF = 1 nanofarad = 10^-9F

1pF = 1 picofarad = 10^-12F

Antigamente, a capacitância era chamada de capacidade eletrostática. Embora esse nome tenha caído em desuso, às vezes ainda o encontramos em alguns textos.

Capacitância de um Condutor Esférico

Consideremos um condutor esférico de raio R, eletrizado com carga Q. supondo-o isolado, seu potencial é dado por

Portanto sua capacitância é dada por:

(IX)

Exemplo 2

Calcule a capacitância de um condutor esférico de raio R = 36 cm, situado no vácuo.

Resolução

No vácuo, nós sabemos que a constante da lei de Coulomb é dada por

k = 9,0. 10⁹ (S.I)

Como R = 36 cm = 36.10^-2m, a capacitância do condutor é dada por:

Avalie a aula