Raiz complexa de um polinômio
- Home
- Raiz Complexa De Um Polinômio
RAÍZES COMPLEXAS DE UM POLINÔMIO
O Teorema Fundamental da álgebra
A ampliação do conceito de número, com a construção do conjunto dos números complexos, nos oferece um sistema no qual toda equação polinomial tem uma raiz. A demonstração dessa propriedade não é simples e foge dos propósitos do nosso curso; ela foi feita em 1799 pelo matemático alemão C. F. Gauss.
|
TEOREMA FUNDAMENTAL DA ÁLGEBRA Todo polinômio P(x) = an xn + an-1 xn-1 + ... + a1 x + a0 (n com coeficientes complexos tem ao menos uma raiz complexa. |
Note que um número real é também um número complexo; então, o teorema aplica-se para polinômios com coeficiente reais. Também, podemos dizer que a equação P(x) = 0 tem ao menos uma raiz real.
Pelo teorema do Fator sabemos que a toda raiz de um polinômio corresponde um fator do 1º grau; então o Teorema Fundamental da álgebra garante que podemos fatorar qualquer polinômio P(x) de grau n como
P(x) = (x - c1) . P1 (x)
onde P1(x) é um polinômio de grau n- 1, e c1 é uma raiz de P(x).
Agora, aplicando o Teorema Fundamental da álgebra para o quociente P1(x), obtemos a fatoração
P(x) = (x - c1) . (x - c2) . P2(x)
onde P2(x) é um polinômio de grau n - 2, e c2 é uma raiz de P1(x).
Esse procedimento aplicado n vezes nos conduz a um quociente Pn(x) de grau zero, que é uma constante não nula, que chamaremos de a. Obtemos, então, a seguinte consequência do Teorema Fundamental da álgebra.
|
TEOREMA DA FATORAÇÃO Se P(x) é um polinômio de grau n > 0, então existem números complexos a, c1, c2, ... , cn (a ≠ 0) tais que P(x) = a (x - c1) (x - c2) . ... . (x - cn) |
O número a é o coeficiente dominante de P(x), isto é, é o coeficiente de xn. Pelo Teorema de Fator, os números c1, c2, ... , cn são as raízes de P(x), ou da equação P(x) = 0. é possível que nem todas são diferentes. Se um fator x - c aparece k vezes na fatoração de P(x), então dizemos que c é uma raiz com multiplicidade k.
|
TEOREMA DAS N RAÍZES Todo polinômio de grau n ≥ 1 tem exatamente n raízes, respeitado que uma raiz de multiplicidade k é contada k vezes. |
Exercícios
1. Determinar todas as raízes da equação x4 - 16 = 0
Resolução
A equação é de grau 4; ela tem exatamente 4 raízes.
Temos:
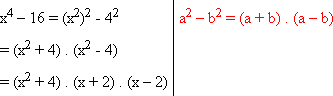
Essa expressão é zero quando um fator é zero.
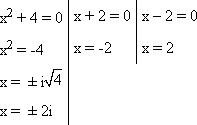
As raízes da equação são 2i, -2i, -2, 2.
2. Resolver a equação x4 - 6x3 + 14x2 - 16x + 8 = 0
Resolução
A equação tem grau 4; ela tem exatamente 4 raízes.
Pelo Teorema das Raízes Racionais sabemos que as possíveis raízes racionais são ± 1, ± 2, ± 4, ± 8.
Usando a divisão sintética, encontramos que 2 é raiz dupla da equação.
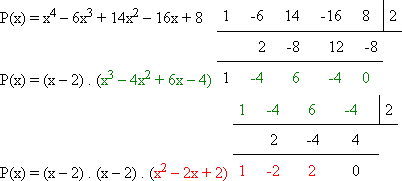
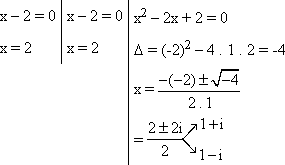
As raízes da equação são 1 + i, 1 - i, 2 (dupla).
3. Construir um polinômio que satisfaz a seguinte descrição:
P(x) tem grau 4, com raízes i, -i, 3 e -3 e com P(0) = -18.
Resolução
Pelo Teorema da Fatoração concluímos que o polinômio desejado tem a seguinte forma:
P(x) = a . (x - i) . [x - (- i)] . (x - 3) . [x - (-3)]
= a (x - i) . (x + i) . (x - 3) (x + 3)
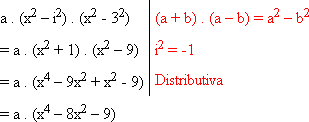
Sendo P(0) = - 18, vem
P(0) = a . (04 - 8 . 02 - 9) = - 18
- 9 a = - 18
a = 2
Então,
P(x) = 2 (x4 - 8x2 - 9)
= 2x4 - 16x2 - 18
Raízes conjugadas
Note nos exercícios resolvidos que as raízes complexas de um polinômio com coeficientes reais, aparecem aos pares.
Quando a + bi é uma raiz, também é raiz seu complexo conjugado a - bi.
|
TEOREMA DAS RAÍZES IMAGINÁRIAS Se um polinômio P(x) com grau n > 0 tem coeficientes reais e se o número complexo z é uma raiz da equação P(x) = 0, então seu complexo conjugado |
Exercício
Formar um polinômio P(x), de grau 3, que tem coeficientes reais e raízes -2 e 2 - i.
Resolução
Sendo 2 - i uma raiz, também é raiz 2 + i, pelo Teorema das Raízes Imaginárias. Então, P(x) é da forma
P(x) = ![]() . [x - (-2)] . [x - (2 - i)] . [x - (2 + i)]
. [x - (-2)] . [x - (2 - i)] . [x - (2 + i)]
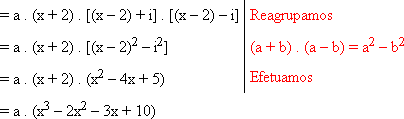
Se, por exemplo, adotarmos a = 1, obtemos
P(x) = x3 - 2x2 - 3x + 10
Observação
Para a determinação do coeficiente dominante a dá-se uma condição, como por exemplo P(2) = 3,
ou P(0) = - 18, ...
Sumário
- O Teorema Fundamental da álgebra- Teorema da fatoração
- Teorema das n raízes
- Teorema das raízes imaginárias
Áreas exclusivas para assinantes






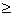 1, an
1, an 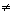 0)
0)