Números imaginários - números complexos
- Home
- Números Imaginários Números Complexos
Números imaginários - números complexos
1. Definições dos números complexos
Vimos na resolução de uma equação do 2º grau que se o discriminante é negativo, ela não admite raízes reais. Por exemplo, a equação
x2 + 9 = 0
não admite raízes reais. Se usarmos os métodos que conhecemos para resolvê-la, obtemos
x2 = -9
x = ± ![]()
mas é inaceitável tal resultado para x; os números negativos não têm raiz quadrada.
Para superar tal impossibilidade e poder, então, resolver todas equações do 2º grau, os matemáticos ampliaram o sistema de números, inventando os números complexos.
Primeiro, eles definiram um novo número
i = ![]()
Isso conduz a i2 = -1. Um número complexo é então um número da forma a + bi onde a e b são números reais.
Para a equação acima fazemos
x = ± ![]()
x = ± ![]()
x = ± ![]() .
. ![]()
x = ± 3 i
As raízes da equação x2 + 9 = 0 são 3i e - 3i.
|
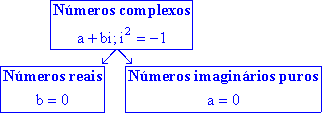
Definição Um número complexo é uma expressão da forma a + bi onde a e b são números reais e i2 = -1. No número complexo a + bi, a é a parte real e b é a parte imaginária. |
Exemplos
|
2 + 5i |
parte real 2 |
parte imaginária 5 |
|
|
parte real |
parte imaginária |
|
12i |
parte real 0 |
parte imaginária 12 |
|
-9 |
parte real -9 |
parte imaginária 0 |
Um número como 12i, com parte real 0, chama-se número imaginário puro. Um número real como -9, pode ser considerado como um número complexo com parte imaginária 0.
Igualdade de números complexos
Os números complexos a + bi e c + di são iguais se suas partes reais são iguais e suas partes imaginárias são iguais, isto é:
a + bi = c + di se ![]()
Exemplos
2 + 5i = ![]()
Se x e y são números reais e x + yi = 7 - 4i, então x = 7 e y = - 4.
2. Aritmética dos números complexos
Adição e Subtração
Adição
|
(a + bi) + (c + di) = (a + c) + (b + d)i |
Para adicionarmos dois números |
Subtração
|
(a + bi) - (c + di) = (a - c) + (b - d)i |
Para subtrairmos dois números |
Exemplos
(3 + 4i) + (- 7 + 8i) = (3 - 7) + (4 + 8) i
= - 4 + 12i
Na prática, fazemos
(3 + 4i) + (-7 + 8i) = 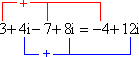
(- 5 + 6i) - (4 - 2i) = (- 5 - 4) + [6 - (- 2)] i
= - 9 + 8i
Na prática fazemos
(-5 + 6i) ![]()
Multiplicação
|
(a + bi) . (c + di) = (ac - bd) + (ad + bc)i |
Multiplicamos números |
Exemplos
|
|
Distributiva |
|
= 6 + i - 12 . (-1) |
-8i + 9i = i e i2 = - 1 |
|
= 6 + i + 12 |
|
|
= 18 + i |
|
|
Distributiva |
|
= - 8 + 2 . (-1) |
-4i + 4i = 0 e i2 = - 1 |
|
= - 8 - 2 |
|
|
= - 10 |
![]() = - 3i . (4) - 3i . (-2i)
= - 3i . (4) - 3i . (-2i)
= - 12i + 6i2
= - 12i + 6 . (-1)
= - 6 - 12i
3. O conjugado e a divisão
Divisão de números complexos é semelhante à racionalização do denominador de uma fração com radicais. Assim, se temos o quociente ![]() nosso objetivo é escrevê-lo na forma a + bi. Para isso, introduziremos inicialmente o conceito de conjugado de um número complexo.
nosso objetivo é escrevê-lo na forma a + bi. Para isso, introduziremos inicialmente o conceito de conjugado de um número complexo.
|
Complexos conjugados O conjugado de um número complexo a + bi é a - bi, e o conjugado de a - bi é a + bi. Os números complexos a + bi e a - bi são chamados complexos conjugados. Para um número complexo z, seu conjugado é representado com |
Exemplos
O conjugado de z = 2 + 3i é ![]() = 2 - 3i
= 2 - 3i
O conjugado de z = 2 - i é ![]() = 2 + 3i
= 2 + 3i
O conjugado de z = 5i é ![]() = - 5i
= - 5i
O conjugado de z = 10 é ![]() = 10
= 10
Quando multiplicamos um número complexo z = a + bi pelo seu conjugado ![]() = a - bi, o resultado que se obtém é um número real não negativo:
= a - bi, o resultado que se obtém é um número real não negativo:
|
z . |
|
|
= a2 - abi + abi - b2i2 |
|
|
= a2 - b2 . (-1) |
A soma dos quadrados |
|
= a2 + b2 |
Usamos essa propriedade para expressar o quociente de dois números complexos na forma a + bi.
|
Dividindo dois números complexos Para escrevermos o quociente |
Exemplo
Vamos escrever o quociente ![]() na forma a + bi.
na forma a + bi.
Multiplicamos o numerador e o denominador pelo conjugado do denominador, para obter um número real no denominador.
![]()
= ![]()
= ![]()
= ![]()
= ![]() i
i
= 1 - i
4. Potências de i
Temos:
|
i0 = 1 |
i4 = i2 . i2 = (-1) . (-1) = 1 |
|
i1 = i |
i5 = i4 . i = 1 . i = i |
|
i2 = -1 |
i6 = i4 . i2 = 1 . (-1) = -1 |
|
i3 = i2 . i = -1 . i = -i |
i7 = i4 . i3 = 1 (-i) = -i |
Observe que as quatro potências de i na coluna da esquerda, repetem-se nos quatro casos seguintes na coluna da direita. Este ciclo
1, i, -1, -i
repete-se indefinidamente.
Então, para simplificar ix para x > 4, buscamos o maior múltiplo de 4 contido em x; por exemplo
i26 = i24 . i2 = (i4)6 . i2 =
= 16 . (-1) =
= -1
i43 = i40 . i3 = (i4)10 . i3
= i10 . (-i)
= -i
5. O caso da raiz quadrada
Sabemos que um número real positivo r tem duas raízes quadradas
![]() e -
e -![]() ,
,
Os números reais negativos também tem duas raízes quadradas. Por exemplo, 2i e -2i são as raízes quadradas de -4 porque
(2i)2 = 22 . i2 = 4 . (-1) = - 4
(- 2i)2 = (- 2)2 . i2 = (- 2)2 . i2 = 4 . (- 1) = - 4
De um modo mais geral, se r > 0 é um número real, o número real negativo - r, tem duas raízes quadradas, porque
(i![]() )2 = i2 . (
)2 = i2 . (![]() )2 = -1 . r = -r
)2 = -1 . r = -r
(-i![]() 2) = (-1) 2 . i2 . (
2) = (-1) 2 . i2 . (![]() )2 = 1 . (-1) . r = -r
)2 = 1 . (-1) . r = -r
Chamamos i![]() de raiz quadrada principal de - r, e usamos o desenho
de raiz quadrada principal de - r, e usamos o desenho ![]() para representá-la; a outra raiz quadrada - i
para representá-la; a outra raiz quadrada - i ![]() é representada com -
é representada com -![]() . Note que as duas raízes quadradas são números complexos imaginários puros, e que são conjugados.
. Note que as duas raízes quadradas são números complexos imaginários puros, e que são conjugados.
|
Raízes quadradas de números negativos Se - r < 0, então as raízes quadradas de - r são i A raiz quadrada principal de - r é i
|
Exemplos
![]() = i
= i ![]() =i
=i
![]() = i
= i![]() = 5i
= 5i
![]() = i
= i![]()
Observação
Devemos ter especial cuidado quando efetuamos operações envolvendo raízes quadradas de números negativos. Quando a e b são positivos vale a propriedade ![]() .
. ![]() =
= ![]() . Mas, quando ambos são negativos a propriedade não é verdadeira. Por exemplo, a definição dada permite-nos escrever
. Mas, quando ambos são negativos a propriedade não é verdadeira. Por exemplo, a definição dada permite-nos escrever
![]() .
. ![]() = i
= i![]() . i
. i![]()
= i2 . ![]() .
. ![]()
=![]()
Entretanto, se usarmos a propriedade temos
![]() .
. ![]() =
= ![]()
Quando multiplicamos radicais de números negativos, devemos em primeiro lugar, escrevê-los na forma i![]() , com r > 0.
, com r > 0.
Exercícios
1. Efetuar as operações indicadas e dar a resposta na forma a + bi.
a) (2 + 3i) + (6 - i)
b) (3 + 5i) - (3 - 7i)
c) (2 + i) (3 + 5i)
d) (- 3 + 2i) . (4 - i)
e) (1 + i) (1 - 2i) i
f) 4i (1 + i) (1 + 2i)
Resolução
a) (2 + 3i) + (6 - i) = ![]()
b) ![]() = 12i
= 12i
c) 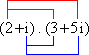 = 6 + 10i + 3i + 5i2
= 6 + 10i + 3i + 5i2
= 6 + 13i + 5 . (-1)
= 6 + 13i - 5
= 1 + 13i
d) 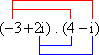 = - 12 + 3i + 12i - 2i2
= - 12 + 3i + 12i - 2i2
= - 12 + 15i - 2 . (-1)
= - 12 + 15i + 2
= - 10 + 15i
e) Vamos, inicialmente, efetuar a multiplicação (1 + i) . (1 - 2 i).
 = 1 - 2i + i - 2i2
= 1 - 2i + i - 2i2
= 1 - i - 2 . (-1)
= 1 - i + 2
= 3 - i
Então,
(1 + i) . (1 - 2i) . i = ![]()
= 3i - i2
= 3i - (-1)
= 3i + 1
= 1 + 3i
f) Vamos inicialmente, efetuar a multiplicação 4i . (1 + i).
![]() = 4i + 4i2
= 4i + 4i2
= 4i + 4 . (-1)
= 4i - 4
= - 4 + 4i
Exercícios
2. Escrever cada um dos quocientes na forma a + bi.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Resolução
a) 
b) 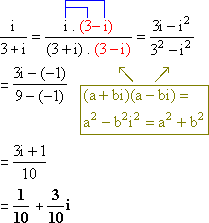
c) 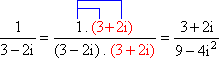
= 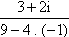 =
=
= 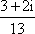
= 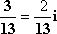
d) 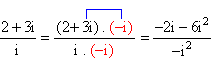
= ![]()
= ![]()
= 6 - 2i
e) ![]()
= ![]()
= ![]()
= ![]()
= ![]()
f) Temos:
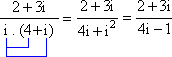
= ![]()
Multiplicando o numerador e o denominador pelo conjugado do denominador vem
![]()
= ![]()
= ![]()
= ![]()
= ![]()
3. Simplificar
a) i15
b) i33
c) (- i)111
d) i218
Resolução
a) Lembre que i4 = 1 e note que
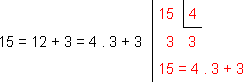
Então, temos
i15 = i4.3+3 = i4.3 . i3
= (i4)3 . i3 = 13 . (- i)
= - i
b) 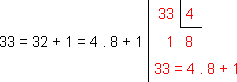
Então, temos
i33 = i4.8+1 = i4.8 . i1
= (i4)8 . i1 = 18 . i
= i
c) Temos:
(-1)111 = (-1 . i)111 = (-1)111 . i111 = - 1 .i111
= - i111
Sendo
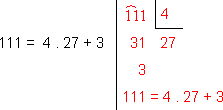
Temos
- i111 = - i4.27+3 = - i4.27 . i3
= - (i4)27 . i3
= - (1)27 . (- i)
= - 1 . (- i)
= i
d) 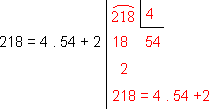
Então temos
i218 = i4.54+2 = i4.54 . i2
= (i4)54 . i2
= 154 . (-1)
= -1
4. Efetue
a) ![]() -
- ![]()
b) ![]() +
+ ![]()
c) ![]()
d) (2 + ![]() ) . (-1 +
) . (-1 + ![]() )
)
Resolução
a) Temos
![]() = i
= i![]() = 5i
= 5i
![]() = i
= i![]() = 3i
= 3i
Então,
![]() -
- ![]() = 5i - 3i = 2i
= 5i - 3i = 2i
b) Temos
![]() = i
= i![]() = 4i
= 4i
![]() = i
= i![]() =7i
=7i
Então,
![]() +
+ ![]() = 4i + 7i = 11i
= 4i + 7i = 11i
c) Temos
![]()
![]()
Então,
![]()
d) Temos
![]()
![]()
Então,
(2 + ![]() ) . (-1 +
) . (-1 + ![]() ) =
) =

= -2 + 6i - 5i + 15i2
= -2 + i + 15(-1)
= -2 + i - 15
= -17 + i
5. Determinar os números reais x e y sabendo que 3x - 4i = 6 + 2yi.
Resolução
Sabemos que números complexos são iguais se suas partes reais são iguais e suas partes imaginárias são iguais.
Então, temos
3x + (- 4) i = 6 + 2yi
![]()
Então, x = 2 e y = - 2.
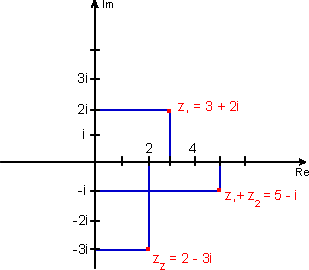
6. Representação dos números complexos
Um número complexo é constituído por duas componentes: a parte real e a parte imaginária. Isso sugere a utilização de dois eixos para representá-lo: um para a parte real e o outro para a parte imaginária. Esses dois eixos chamam-se eixo real e eixo imaginário, respectivamente. O plano determinado por esses dois eixos chama-se plano complexo.
Para desenharmos o gráfico do número complexo a + bi, marcamos o ponto (a; b) no plano.
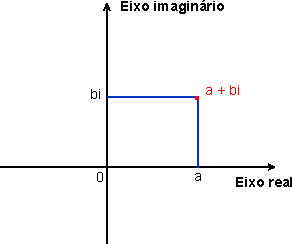
Exemplo
7. Módulo de número complexo
O módulo (ou valor absoluto) do número complexo a + bi é distância de a + bi à origem do plano complexo. Usando o Teorema de Pitágoras, concluímos que a distância de (a; b) a (0; 0) é ![]() .
.
|
Definição O módulo (ou valor absoluto) do complexo z = a + bi é | z | = |
Exemplos
O módulo do número complexo - 3 + 4i é
|-3 + 4i| = ![]() =
= ![]() = 5
= 5
O módulo do número complexo 7 + 4i é
|7 + 4i| = ![]() =
= ![]()
Sumário
- Definições- Igualdade de números complexos
- Aritmética dos números complexos
- O conjugado e a divisão
- Potências de i
- O caso da raiz quadrada
- Representação dos números complexos
- Módulo de número complexo
Áreas exclusivas para assinantes






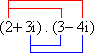 = 6 - 8i + 9i -12i2
= 6 - 8i + 9i -12i2 = - 8 - 4i + 4i + 2i2
= - 8 - 4i + 4i + 2i2