Função Quadrática
- Home
- Função Quadrática
FUNÇÃO QUADRÁTICA
Definições
Uma função definida por um polinômio do 2º grau se chama função quadrática. São exemplos de função quadrática em x:
f(x) = - 2 x2 + x + 1
g(x) = 4 x2 - 5
h(x) = x2
Definição
Uma função quadrática é uma função da forma
f(x) = a x2 + b x + c
onde a, b e c são números reais a ≠ 0.
O gráfico da função quadrática
Entre as equações quadráticas a mais simples é f(x) = x2. O seu gráfico servirá como base para construirmos os gráficos de outras equações quadráticas.
Inicialmente, apresenta-se uma simetria. Temos:
f(-2) = f(2) = 4
f(-1) = f(1) = 1
De um modo geral,
f(-x) = (-x)2 = x2 = f(x)
isto é, para todo x temos
f(-x) = f(x)
|
Função par Quando uma função f satisfaz, para todo x do seu domínio, a propriedade f(-x) = f(x) ela se chama função par, e seu gráfico é simétrico em relação ao eixo-y. |
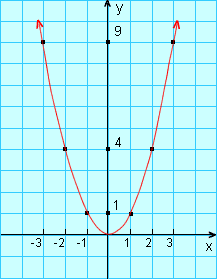
Vamos construir uma tabela com pares ordenados que são as coordenadas de pontos do gráfico da equação y = x2. Quando marcamos esses pontos em um sistema de coordenadas e os unimos em uma curva contínua, obtemos o gráfico da função f(x) = x2.
|
x |
y = x2 |
(x; y) |
|
-3 |
9 |
(-3; 9) |
|
-2 |
4 |
(-2; 4) |
|
-1 |
1 |
(-1; 1) |
|
0 |
0 |
(0; 0) |
|
1 |
1 |
(1; 1) |
|
2 |
4 |
(2; 4) |
|
3 |
9 |
(3; 9) |
Observação:
Podemos ter uma maior precisão no gráfico marcando mais pontos. Como não podemos marcar uma infinidade de pontos, admitimos uma certa dose de confiança de que o gráfico é aquele que desenhamos.
A curva obtida se chama parábola e toda equação quadrática y = a x2 + b x + c tem uma parábola como gráfico. O domínio da função é o conjunto dos números reais e seu conjunto imagem depende dos valores de a, b e c. Para a função f(x) = x2 o conjunto imagem é constituído por todos y ≥ 0.
Uma propriedade importante dessa parábola é que ela é simétrica em relação a uma reta vertical que se chama eixo de simetria. O gráfico da equação y = x2 é simétrico em relação ao eixo-y. Essa simetria deve-se ao fato de que f(-x) = (-x)2 = x2 = f(x) e que, portanto, a função é par.
A parábola tem um ponto de retorno, que se chama vértice. O vértice é a intersecção da parábola com o eixo de simetria.
No gráfico da equação y = x2 o vértice tem coordenadas (0; 0) e o valor mínimo da função é 0.
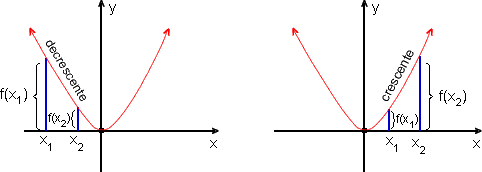
Note que, avançando da esquerda para a direita, a curva "desce" até a origem e depois "sobe". Dizemos que f é decrescente e que f é crescente.
|
|
|
|
f(x) = x2 é decrescente para x |
f(x) = x2 é crescente para x |
FUNÇÃO CRESCENTE E FUNÇÃO DECRESCENTE
f é crescente sobre o intervalo I se f(x1) < f(x2) sempre que x1 < x2, em I
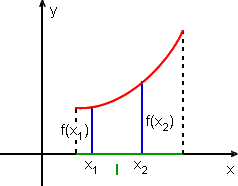
f é decrescente sobre o intervalo I se f(x1) > f(x2) sempre que x1 < x2, em I
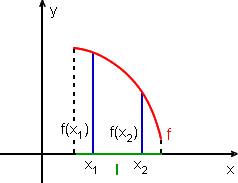
Exemplo
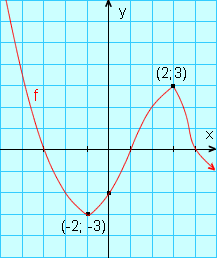
Para a função f cujo gráfico está na figura, temos:
|
intervalo |
crescimento/decrescimento |
|
x ≤ - 2 -2 ≤ x ≤ 2 x ≥ 2 |
f decresce f cresce f decresce |
Podemos usar o gráfico da equação y = x2 para construirmos os gráficos de outras funções quadráticas. Por exemplo, os gráficos das funções y = x2 + 1 e y = x2 - 1 podem ser obtidos do gráfico da equação y = x2 por translações verticais desse gráfico.
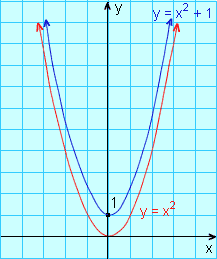
O gráfico de y = x2 + 1 é obtido deslocando o gráfico de y = x2 + 1 unidade para cima.
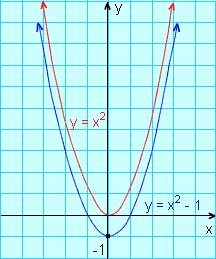
O gráfico de y = x2 -1 é obtido deslocando o gráfico de y = x2 1 unidade para baixo.
Também, podemos construir os gráficos das funções y = (x - 1)2 e y = (x + 1)2 a partir do gráfico de y = x2, fazendo translações horizontais desse gráfico.
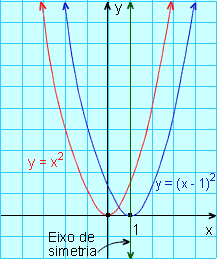
O gráfico de y = (x - 1)2 é obtido deslocando o gráfico de y = x2 1 unidade para direita. O vértice está em (1;0) e o eixo de simetria é a reta x = 1.
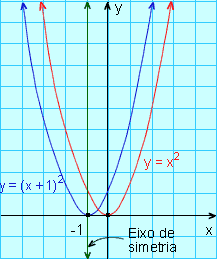
O gráfico de y = (x + 1)2 é obtido deslocando o gráfico de y = x2 uma unidade para a esquerda. O vértice está em (-1;0) e o eixo de simetria é a reta x = - 1.
Nos gráficos que construímos até aqui, o coeficiente de x2 é 1. Se o coeficiente é -1, o efeito sobre o gráfico é uma reflexão em relação ao eixo-x.
Então, para a função y = - x2 o domínio continua sendo o conjunto dos números reais, mas o conjunto imagem é o conjunto dos números reais y tais que y ≤ 0.
O vértice está em (0; 0) e 0 é valor máximo da função.
|
x |
y = - x2 |
(x; y) |
|
-3 |
-9 |
(-3; -9) |
|
-2 |
-4 |
(-2; -4) |
|
-1 |
-1 |
(-1; -1) |
|
0 |
0 |
(0; 0) |
|
1 |
-1 |
(1; -1) |
|
2 |
-4 |
(2; -4) |
|
3 |
-9 |
(3; -9) |
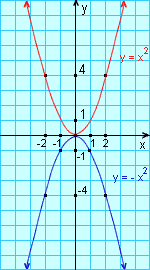
O gráfico de y = - x2 é obtido por reflexão do gráfico de y = x2 em torno do eixo-x.
Vimos que o gráfico de y = x2 tem um ponto de retorno no vértice; ele se dobra "para cima". Dizemos que a curva tem concavidade para cima. O gráfico de y = - x2 se dobra para baixo; dizemos que a curva tem concavidade para baixo.
Quando o coeficiente a em y = a x2 é diferente de 1, o gráfico dessa função pode ser obtido multiplicando a ordenada y, dos pontos de y = x2, pelo número a, como nos exemplos abaixo.
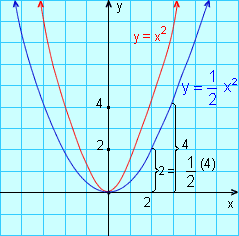
Cada ordenada é a metade da ordenada do gráfico de y = x2.
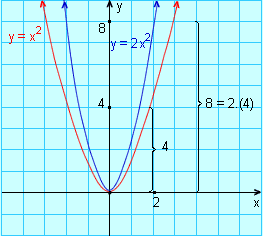
Cada ordenada é o dobro da ordenada do gráfico de y = x2.
Note que o gráfico de y = 2 x2 está "mais levantado" em relação ao gráfico de y = x2; o gráfico de y = 2 x2 "se afasta" do eixo-x. O gráfico de y = ![]() x2 "se aproxima" do eixo-x.
x2 "se aproxima" do eixo-x.
Exercícios
1. Desenhar o gráfico da função y = - x2 + 3. Dizer onde a função é crescente ou decrescente. Qual é o conjunto-imagem da função?
Resolução
Partimos do gráfico de y = - x2; deslocando-o de 3 unidades "para cima", obtemos o gráfico de y = - x2 + 3.
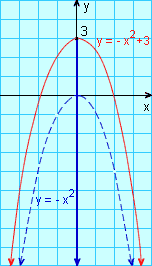
A função y = - x2 + 3 é crescente para x ≤ 0 e é decrescente para x ≥ 0. Seu conjunto-imagem é constituído por todos y tais que y ≤ 3.
2. Desenhar o gráfico da função y = f(x) = (x + 2)2 - 2.
Resolução
Partimos do gráfico da função y = x2. Deslocando-o "para a esquerda" de 2 unidades, obtemos o gráfico de y = (x + 2)2; depois, deslocando-o "para baixo" de 2 unidades, obtemos o gráfico de y = f(x) = (x + 2)2 - 2.
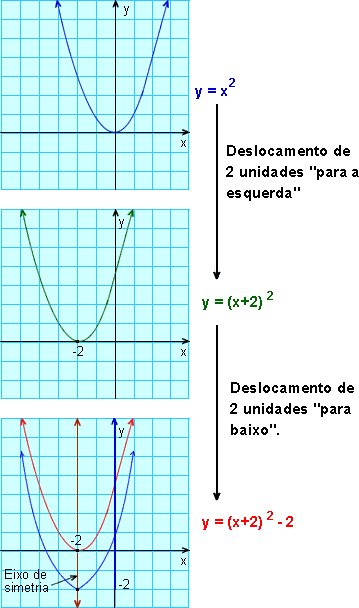
Note que o conjunto-imagem da função f é constituído por todos y tais que y ≥ -2.
3. Desenhar o gráfico da parábola y = 2 (x - 2)2 + 1.
Resolução
Começamos com o gráfico de y = 2 x2; deslocando-o 2 unidades "para a direita", obtemos o gráfico de y = 2 (x - 2)2.
Então, deslocando-o 1 unidade "para cima" obtemos o gráfico de y = 2 (x - 2)2 = 1.
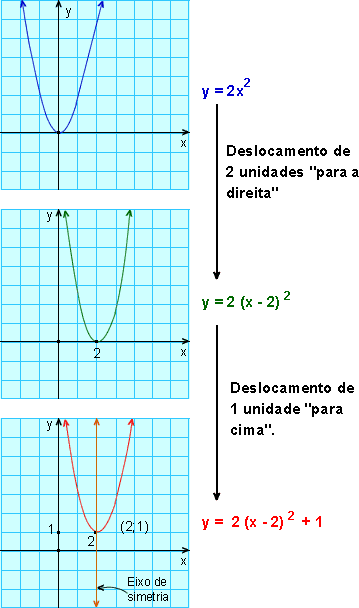
O vértice da parábola é o ponto V (2; 1) e o eixo de simetria tem equação x = 2.
Um resumo
Gráfico da equação y =a (x - h)2 + k.
O gráfico da equação y = a (x - h)2 + k pode ser obtido do gráfico da equação y = a x2, deslocando-o h unidades horizontalmente e k unidades verticalmente.
- O deslocamento horizontal é "para a direita" se h > 0, e é "para esquerda" se h < 0.
- O deslocamento vertical é "para cima" se k > 0, e é "para baixo" se k < 0.
O vértice é o ponto V (h ; k); o eixo de simetria é a reta (vertical) de equação x = h.
Se a < 0, o vértice é o ponto "mais alto" da parábola e sua concavidade está voltada "para baixo"; se a > 0, o vértice é o ponto "mais baixo" da parábola e sua concavidade está voltada "para cima".
Completando o quadrado
Vamos desenhar o gráfico da função f(x) = 2 x2 - 4 x + 5.
Note que o coeficiente de x2 não é 1; então, fatoramos esse coeficiente (colocamos em evidência) nos termos que envolvem x, e em seguida, "completamos o quadrado" dentro dos parênteses.
|
f(x) = 2x2 - 4x + 5 |
|
Colocamos 2 em evidência nos termos em x |
|
= 2 . (x2 - 2x) + 5 |
||
|
= 2 . (x2 - 2x + 1) + 5 - 2 |
Completamos o quadrado na expressão dentro dos parênteses |
|
|
= 2 . (x - 1)2 + 3 |
Então, a função está escrita na forma y = a (x - k)2 + h, e sabemos como desenhar o seu gráfico.
Começamos com o gráfico de y = 2 x2, deslocando-o 1 unidade "para a direita" e, em seguida, 3 unidades "para cima". O vértice da parábola resultante é o ponto (1; 3). Sendo a = 2 > 0, a concavidade está voltada "para cima".
O gráfico está desenhado na figura abaixo; observe que f(0) = 5; isto significa que a parábola encontra o eixo-y no ponto (0; 5) ou ainda, que o intercepto-y é o ponto (0; 5). O eixo de simetria é a reta de equação x = 1.
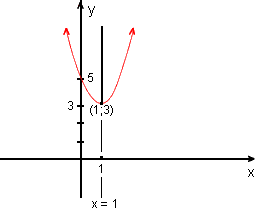
A técnica que acabamos de usar chama-se completar o quadrado.
Esse processo pode ser resumido como segue.
|
Completar o quadrado Para completar o quadrado em expressões quadráticas da forma x2 + b x, somamos o quadrado da metade de b, o coeficiente de x: Então, x + bx + |
Completando o quadrado, podemos escrever qualquer equação quadrática na forma y = a (x - h)2 + k. E, a partir dele, podemos localizar o vértice da parábola (h; k) e escrever a equação do eixo de simetria x = h.
Máximo e mínimo
Vimos que partindo da equação f(x) = a x2 + b x + c podemos, completando o quadrado, chegar à equação f(x) = a (x - h)2 + k. O gráfico dessa equação pode ser obtido do gráfico da equação y = a x2, com deslocamentos horizontais ou verticais. O vértice da parábola resultante é o ponto (h; k). Se a > 0, a parábola tem a concavidade "voltada para cima". Mas se a < 0, a concavidade está "voltada para baixo".
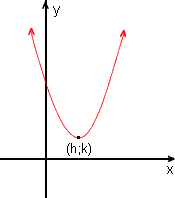
f(x) = a . (x - h)2 + k
a > 0, h > 0, k > 0
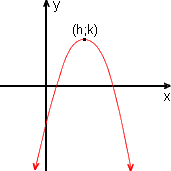
f(x) = a . (x - h)2 + k
a < 0, h > 0, k > 0
Observe na figura que se a > 0, então o ponto "mais baixo" da parábola é o vértice (h; k), de modo que o mínimo valor da função ocorre quando x = h e esse valor mínimo é f(h) = k. De modo análogo, se a < 0, então o ponto "mais alto" da parábola é o vértice (h ; k), de modo que o máximo valor da função ocorre quando x = h e esse valor máximo é f(h) = k.
|
Valor máximo - valor mínimo A função quadrática f(x) = a x2 + b x + c pode ser escrita na forma f(x) = a (x - h)2 + k completando o quadrado. O gráfico da função é uma parábola com vértice (h ; k); a parábola tem a concavidade "voltada para baixo" se a > 0 e "para cima" se a < 0. Se a > 0, então o valor mínimo da função ocorre quando x = h e esse valor é f(h) = k. Se a < 0, então o valor máximo da função ocorre quando x = h e esse valor é f(x) = k. |
Exercícios
1. Dada a função quadrática f:
a) Escrevê-la na forma f(x) = a (x - h)2 + k.
b) Esboce o seu gráfico.
c) Determine o valor máximo ou o valor mínimo de f.
f(x) = x2 + 4x - 3
Resolução
a) Completando o quadrado, temos
f(x) = (x2 + 4x + 4) - 3 - 4
= (x + 2)2 - 7
b) O gráfico é uma parábola de vértice (- 2; - 7) e concavidade voltada "para cima"
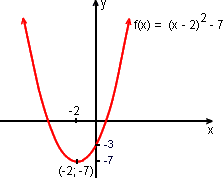
c) A função tem um valor mínimo que é f(- 2) = -7.
2. Dada a função quadrática f:
a) Escrevê-la na forma f(x) = a (x - h)2 + k.
b) Esboce o seu gráfico.
c) Determine o valor máximo ou o valor mínimo de f.
f(x) = - x2 + x - 2
Resolução
a) Completando o quadrado temos:
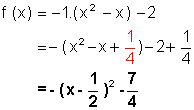
b) O gráfico é uma parábola com vértice ![]() , e concavidade voltada "para baixo".
, e concavidade voltada "para baixo".
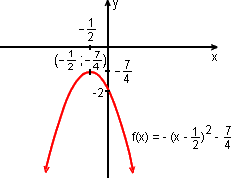
c) A função tem um valor máximo que é 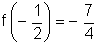 .
.
Transformação da equação f(x) = ax2 + bx + c
Quando desejamos desenhar o gráfico da função quadrática f(x) = ax2 + bx + c é conveniente escrevê-la na forma f(x) = a (x - h)2 + k. Se, entretanto, desejamos o valor mínimo ou o valor máximo da função quadrática, a fórmula f(x) = ax2 + bx + c pode, com vantagem, dar a resposta.
Então, completando o quadrado para a função quadrática geral, temos:
|
f(x) = ax2 + bx + c |
|
|
|
= a |
Colocamos a em evidência nos termos em x |
|
|
= a |
Completamos o quadrado |
|
|
= a |
|
E, escrevendo b2 - 4 a c = Δ, vem
![]()
A equação obtida é da forma f(x) = a (x - h)2 + k, com h = ![]() e k =
e k = ![]() ; o máximo ou o mínimo valores ocorre quando x =
; o máximo ou o mínimo valores ocorre quando x = ![]() .
.
|
Máximo ou mínimo valores de uma função quadrática O valor máximo ou o valor mínimo da função quadrática f(x) = ax2 + bx + c ocorre em x = Se a > 0, então o valor mínimo é m = Se a < 0, então o valor máximo é M = |
Exercícios
1. Dada a função quadrática f determine o valor máximo ou o valor mínimo.
f(x) = ![]() x2 + x + 2
x2 + x + 2
Resolução
![]() é uma função quadrática com a =
é uma função quadrática com a = ![]() , b = 1 e c = 2.
, b = 1 e c = 2.
Sendo a < 0, a função tem um valor máximo, que ocorre em
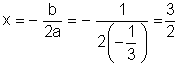
Esse valor máximo é
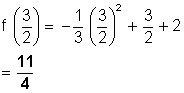
2. Dada a função quadrática f determine o valor máximo ou o valor mínimo.
f(x) = x2 - 10x + 21
Resolução
f(x) = x2 - 10x + 21 é uma função quadrática com a = 1, b = -10 e c = 21.
Sendo a > 0, a função tem um valor mínimo, que ocorre em
![]()
Em valor mínimo é
f(5) = 52 - 10 . 5 + 21
= - 4
3. Uma bola é lançada verticalmente para cima, do nível do solo, com uma velocidade igual a 20 m/seg. A altura s da bola, t segundos após o lançamento é dada por s = 20 t - 8 t2. Qual é a altura máxima que a bola alcança?
Resolução
Note que s é uma função quadrática de t:
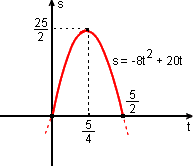
s = - 8t2 + 20t
onde a = - 8, b = 20 e c = 0; sua concavidade está voltada "para baixo"; ela tem um valor máximo que ocorre em
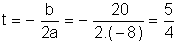
O valor máximo de s é
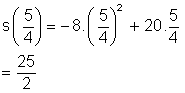
Então, a bola alcança a altura máxima 12,5 m após 1,2 segundos do lançamento
Inequação do 2º grau
Consideremos a função quadrática f(x) = x2 - 4 x + 3, na qual a = 1, b = -4 e c = 3.
O seu discriminante é
Δ = b2 - 4ac = (-4)2 - 4 . 1 . 3 = 4,
isto é, Δ > 0
Se resolvermos, então, a equação f(x) = 0 ou x2 - 4x + 3 = 0, ela admitirá duas raízes:
x = ![]() =
= ![]()
Isto significa que a parábola de equação y = x2 - 4x + 3 cruza o eixo-x em dois pontos (interceptos-x): (1; 0) e (3; 0)
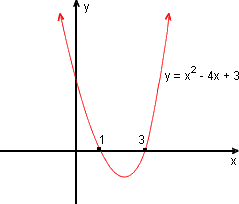
Seja agora a função quadrática f(x) = x2 - 6x + 9, na qual a = 1, b = - 6 e c = 9.
O seu discriminante é
Δ = b2 - 4ac = (-6)2 - 4 . 1 . 9 = 0,
isto é, Δ = 0
Se resolvermos, então, a equação f(x) = 0 ou x2 - 6 x + 9 = 0, ela admitirá uma única raiz:
x = ![]()
Isto significa que a parábola de equação y = x2 - 6 x + 9 toca (tangencia) o eixo-x em um ponto: (3; 0)
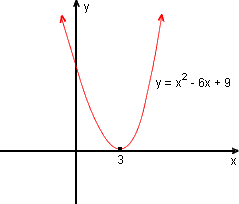
Seja finalmente a função quadrática f(x) = x2 + x + 2, na qual a = 1, b = 1 e c = 2.
O seu discriminante é
Δ = b2 - 4ac = 12 - 4 . 1 . 2 = 7,
isto é, Δ < 0
Se resolvermos, então, a equação f(x) = 0 ou x2 + x + 2 = 0, ela não admitirá raízes.
Isto significa que a parábola de equação y = x2 + x + 2 não cruza e nem toca o eixo-x.
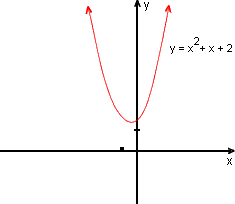
O discriminante e a parábola
Δ = b2 - 4ac > 0
A equação ax2 + bx + c = 0 admite duas raízes reais.
O gráfico de y = ax2 + bx + c cruza o eixo-x em dois pontos.
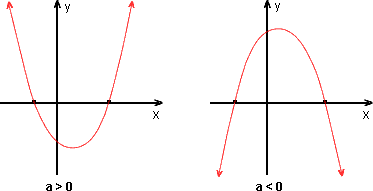
Δ = b2 - 4ac = 0
A equação ax2 + bx + c = 0 admite uma única raiz real.
O gráfico de y = ax2 + bx + c toca (tangencia) o eixo-x.
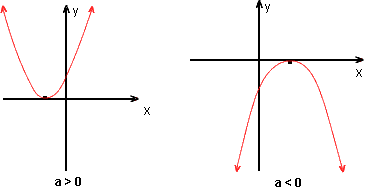
Δ = b2 - 4ac < 0
A equação ax2 + bx + c = 0 não tem raízes reais.
O gráfico de y = ax2 + bx + c não cruza e nem toca o eixo-x.
Agora, vamos resolver inequações do 2º grau; elas podem ser resolvidas empregando o gráfico da função quadrática associada.
Exemplo
Vamos resolver a inequação x2 + 2x - 3 < a.
Seja a parábola y = f(x) = x2 + 2x - 3.
A concavidade da parábola está "voltada para cima" a = 1 > 0
Interceptos
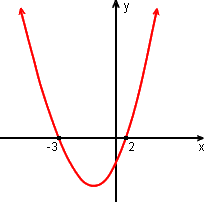
 = b2 - 4ac =22 - 4 . 1 . (-3) = 16
= b2 - 4ac =22 - 4 . 1 . (-3) = 16
raízes = ![]()
Os interceptos-x são (-3; 0) e (1; 0)
Gráfico
y = x2 + 2x - 3 é negativo quando a parábola está abaixo do eixo-x; isto é, quando x está entre -2 e 3.
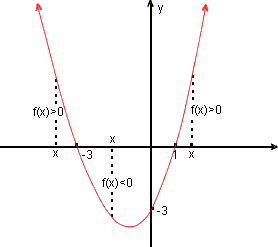
A solução conota de todos os números reais tais que -2 < x < 3, ou o conjunto solução é
S = {x 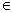
![]() | -2 < x < 3}
| -2 < x < 3}
Note que a partir da figura acima, também podemos resolver a inequação x2 + 2x - 3 > 0;
y = x2 + 2x - 3 é positivo quando a parábola está acima do eixo-x, isto é, quando x < - 3 ou x > 1.
Exercícios
1. Resolva a inequação do 2º grau.
x2 + x - 6 < 0
Resolução
a = 1: concavidade voltada "para cima"
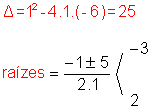
y = x2 + x - 6 é positivo quando a parábola está acima do eixo - x
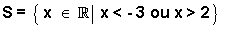
2. Resolva a inequação do 2º grau.
(2x + 1) . (3x - 4) < 0
Resolução
Temos:
![]()
6x2 - 8x + 3x - 4 < 0
6x2 - 5x - 4 < 0
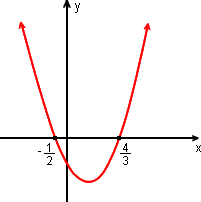
a = 6: concavidade voltada "para cima".
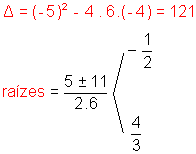
y = 6x2 - 5x - 4 é negativo quando a parábola está abaixo do eixo - x
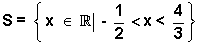
3. Resolva a inequação do 2º grau.
2x2 + ![]() x + 1 < 0
x + 1 < 0
Resolução
a = 2: concavidade voltada "para cima".
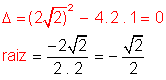
![]() é negativo quando a parábola está abaixo do eixo-x
é negativo quando a parábola está abaixo do eixo-x
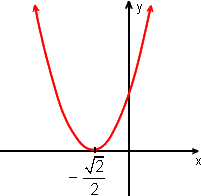
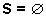
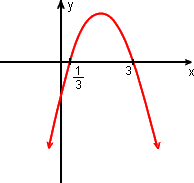
4. Resolva a inequação do 2º grau.
x2 - x + 14 > 4x2 - 11x + 17
Resolução
Temos:
x2 - x + 14 > 4x2 - 11x + 17
x2 - x + 14 - 4x2 + 11x - 17 > 0
- 3x2 + 10x - 3 > 0
a = - 3: concavidade voltada "para baixo".
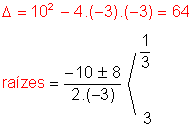
y = - 3x2 + 10x - 3 é positivo quando a parábola está acima do eixo - x.
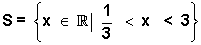
5. Resolva a inequação do 2º grau.
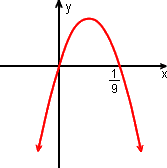
- 9x2 + x > 0
Resolução
a = - 9: concavidade voltada "para baixo"
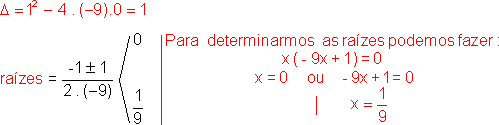
y = - 9x2 + x é positivo quando a parábola está acima do eixo - x.
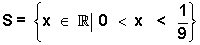
Sumário
- Definição da função quadrática
- Função par
- Função crescente e função decrescente
- Gráfico da equação y =a (x - h)2 + k.
- Completando o quadrado
- Máximo e mínimo
- Transformação da equação f(x) = ax2 + bx + c
- O discriminante e a parábola
Áreas exclusivas para assinantes






 0
0 0
0