Polinômios
- Home
- Polinômios
Estudo dos polinômios
Chama-se polinômio na variável real x, toda a expressão da forma p(x) = a0xn + a2xn-1 + a2xn-2 + an-1x1 onde N  .
.
Raiz ou zero do Polinômio
Trata-se do valor de P(x) que faz: P(x) = 0
A existência das raízes da equação P(x) = 0 é garantida pelo teorema fundamental da álgebra, atribuído a D´Alembert: "Toda equação polinomial tem pelo menos uma raiz, real ou complexa”.
Valor Numérico de um polinômio
Para x = b é representado por P(b) = a0 . bn + a1 . bn-1 + a2 . bn-2 +an
Grau de um Polinômio
Chama-se grau de um polinômio P(x) ≠ 0, o número n  tal que n é o maior valor de n
tal que n é o maior valor de n  , para o qual an ≠ 0 (onde n = 0,1,2,3 ...)
, para o qual an ≠ 0 (onde n = 0,1,2,3 ...)
Exemplos
P(x) = 2x3 - 3x + 1 Grau 3
P(x) = 5 Grau 0
P(x) = x2 - 3x + 7 Grau 2
Polinômio Nulo
Diz-se que um polinômio P(x) é identicamente nulo se P(a) = 0 para qualquer a.
Operações com Polinômios
Soma / Subtração de Polinômios
Da álgebra elementar temos que nós só podemos somar e/ou subtrair termos semelhantes, ou seja, termos que possuam expoentes iguais.
Exemplos
P(x) = 3x4 - 7x3 + 5x2 + 12x - 8
Q(x) = x4 - 12x2 + 7x + 2
P(x) + Q(x) = 4x4 - 7x3 - 7x2 + 19x - 6
P(x) - Q(x) = 2x4 - 7x3 + 17x2 + 5x - 10
Multiplicação de Polinômios
Exemplo
(2x2 - 7x + 4) . (x3 + 2x) = 2x5 + 4x3 - 7x4 - 14x2 + 4x3 + 8x
Divisão de Polinômios
Método da chave:
Exemplo
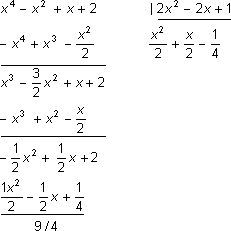
Assim o Q(x) = 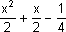 é o quociente da divisão e R(x)= 9/4 é o resto.
é o quociente da divisão e R(x)= 9/4 é o resto.
Teoremas
Teorema do Resto
O resto da divisão de um polinômio p (x) por x – c é o valor numérico de p(x) em c, isto é, o resto é p (c).
Exemplo
Calcular o resto da divisão de f = x3 - 2x2 + 3 por x - 1.
r = f(1) = 1 – 2 + 3 = 2
Teorema de D´Alembert
Um polinômio p(x) é divisível por x – c se e somente se p (c) = 0.
Dispositivo de Briot – Ruffini
Dividir x3 - 7x - 6 por x - 3. Observando que x3 - 7x - 6 = x3 + 0x2 - 7x - 6, temos:
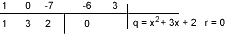
Sumário
- Raiz ou zero- Valor Numérico
- Grau de um Polinômio
- Operações com Polinômios
- Teorema do Resto
- Teorema de D’Alembert
- Dispositivo de Briot – Ruffini
Áreas exclusivas para assinantes





