Função inversa
- Home
- Função Inversa
FUNÇÃO INVERSA
Função um-para-um
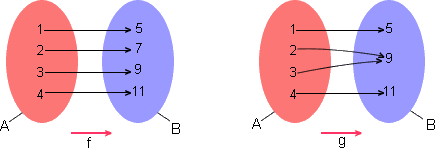
Na figura, observe as funções f e g.
|
|
|
|
f é um-para-um |
g não é um-para-um |
Note que, em f, quaisquer dois números do domínio A têm imagens diferentes mas, em g, 2 e 3 têm a mesma imagem 9. Em símbolos, g(2) = g(3) mas f(x1) 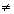 f(x2) para quaisquer x1
f(x2) para quaisquer x1 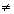 x2.
x2.
|
Função um-para-um Uma função f com domínio A chama-se um-para-um (1-1) se quaisquer dois elementos de A não têm a mesma imagem, isto, é, f(x1) ≠ f(x2) sempre que x1 ≠ x2. |
O gráfico de uma função 1-1
Se uma reta horizontal encontra o gráfico de uma função f em mais do que um ponto,
então f não é 1-1 ![]()
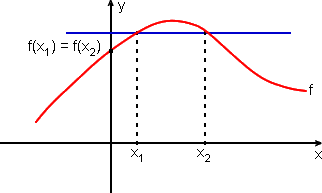
Note que existem x1 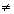 x2 tais que f(x1) = f(x2), o que contraria a definição de função 1-1.
x2 tais que f(x1) = f(x2), o que contraria a definição de função 1-1.
Podemos, então, estabelecer um critério geométrico (gráfico) para decidir se uma função é 1-1.
|
Teste da horizontal Uma função f é 1-1 se nenhuma reta horizontal encontra o seu gráfico mais do que uma vez. |
Exemplos
Seja a função f(x) = x2 cujo domínio é o conjunto de todos os números reais.
Note que f(-1) = f(1), isto é, 1 e -1 têm a mesma imagem; a função não é 1-1.
f(x) = x2 não é 1-1
Se, entretanto, restringirmos o domínio de f, podemos conseguir uma função 1-1.
Definindo
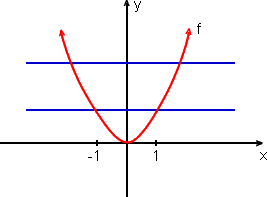
g(x) = x2, x ≥ 0
então, g é 1-1; veja o teste da horizontal.
g(x) = x2 (x ≥ 0) é 1-1
Função inversa
|
Definição Seja f uma função 1-1, com domínio A e conjunto imagem B. Então, sua função inversa f -1 tem domínio B e conjunto imagem A e é definida por f -1(y) = x ⇔ f(x) = y para todo y em B |
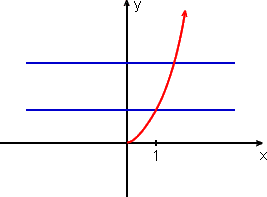
A definição diz que se f leva x em y:
f(x) = y ![]()
então f -1 leva y em x:
f -1(y) = x 
Note que f -1 "desfaz" o efeito de f.
Também, temos
domínio de f -1 = conjunto imagem de f
conjunto imagem de f -1 = domínio de f
Exemplo
Seja a função f definida pelo diagrama abaixo.
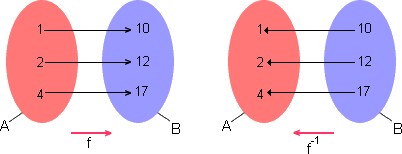
Temos:
f(1) = 10
f(2) = 12
f(4) = 17
f -1(10) = 1
f -1(12) = 2
f -1(17) = 4
Como determinar a inversa
Inicialmente observe que da definição de função inversa temos
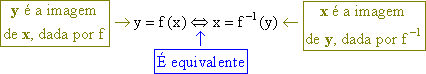
Então, se y = f(x) é a fórmula para f, a fórmula para a inversa f -1 é x = f -1(y). Para obtê-la, resolvemos a equação y = f(x) para x (determinamos x em termos de y). Em seguida, trocamos as letras x e y, e chegamos a y = f -1(x), que é a fórmula desejada para a inversa f -1.
|
Determinação da fórmula da inversa 1. Escrevemos y = f(x) 2. Resolvemos essa equação para x (em termos de y) 3. Trocamos as letras, x por y e y por x. O resultado é a equação y = f -1(x), para a função inversa. |
Exemplo
Vamos determinar a inversa da função f(x) = 2x - 3.
Inicialmente, escrevemos y = f(x).
y = 2x - 3
Resolvemos essa equação para x:
2x = y + 3
x = ![]()
Finalmente, trocamos as letras x e y:
y = ![]()
Então, a função inversa é f -1(x) = ![]()
Exercícios
1. Seja a função f(x) = ![]()
Calcular (f -1 o f) (x).
Resolução
(f -1o f)(x) = f -1(f (x)) = f -1![]()
= ![]()
= ![]()
= x
Observação: De um modo geral, sempre se tem
(f -1 o f) (x) = (f o f -1) (x) = x
O gráfico da inversa
Se para a função f temos f(a) = b, então para a inversa f -1, f -1(b) = a.
Isto significa que se o ponto (a; b) está no gráfico de f, o ponto (b; a) está no gráfico de f -1. Esses dois pontos (a; b) e (b; a) guardam uma propriedade geométrica; são simétricos em relação à reta y = x, isto é, o ponto (b; a) pode ser obtido do ponto (a; b) por reflexão em y = x.
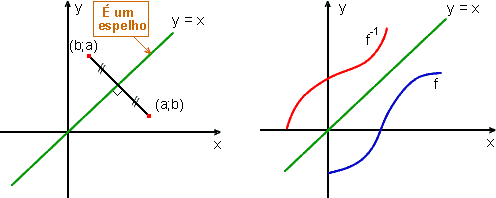
|
O gráfico de f -1 é obtido refletindo o gráfico de f em y = x. |
Exemplo
Consideremos a função f(x) = x2, x ≥ 0, e vamos determinar sua inversa.
Temos
y = x2
x = ![]() (x ≥ 0)
(x ≥ 0)
Trocando as letras
y = ![]()
e a função inversa é f -1(x) =![]()
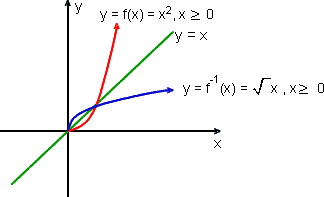
Sumário
- Função um-para-um- O gráfico de uma função 1-1
- Função inversa
- Como determinar a inversa
- O gráfico da inversa
Áreas exclusivas para assinantes