Equações e Inequações - Sistemas de equações
- Home
- Equações E Inequações Sistemas De Equações
Equações e Inequações - Sistemas de equações
Equação do 1º Grau
Toda equação na variável x do tipo (ou redutível a) ax + b = 0 com a ≠ 0 e a , b ∈ R é denominada equação polinomial do 1º grau em x.
![]()
Exemplos
3x - 6 = 0
3x = 6
![]()
x = 2
(é raiz, solução ou zero da equação; note que x = 2 o único valor de x que torna verdadeira a igualdade.)
Inequação do 1º Grau
Conceito de desigualdade
Os símbolos que representam desigualdades são: ≠, >, < e toda sentença aberta (que possui pelo menos uma variável) onde apareça uma desigualdade é uma inequação.
Uma propriedade importante das desigualdades é:
a > b ⇔ - a < - b
Ou seja, multiplicando-se ou dividindo-se uma desigualdade por um número negativo "inverte-se o sentido" da desigualdade.
Exemplos
3x - 5 < x + 7
3x - x < 7 + 5
2x < 12
x < 6
![]()
Equação do 2º Grau
Toda equação na variável x do tipo (ou redutível a) ax2 + bx + c = 0 onde ![]() ; b ,
; b , ![]() , é denominada equação polinomial do 2º grau.
, é denominada equação polinomial do 2º grau.
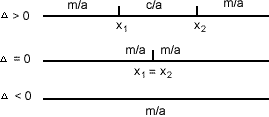
Discriminante:
Δ = b² - 4ac
Se Δ > 0 temos se Δ ![]() = 0 temos
= 0 temos ![]() se Δ < 0 não existem raízes reais.
se Δ < 0 não existem raízes reais.
Se x1 e x2 são as raízes da equação ax2 + bx + c = 0 , então
![]()
![]()
Exemplos
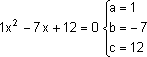
Δ = b² - 4 . a . c
Δ = 49 - 4 . 1 . 12
Δ = 49 - 48
Δ = 1
![]()
Inequação do 2º Grau
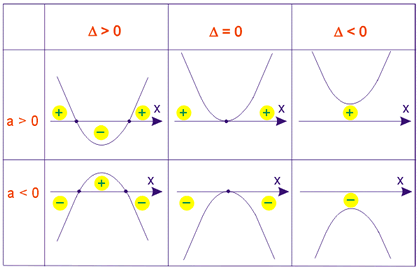
Estudo da variação dos sinais das imagens da função do 2º grau.
Seja a função f: |![]()
![]()
![]() | f(x) = ax2 + bx + c = 0 (a ≠ 0).
| f(x) = ax2 + bx + c = 0 (a ≠ 0).
Seu gráfico é uma parábola que se comporta conforme a tabela abaixo:
ou:
Exemplo
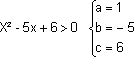
1º Cálculo das raízes
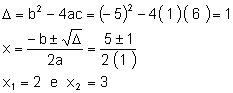
2º Esboço da Parábola

3º Análise do sinal
x² - 5x + 6 > 0 p/ x < 2 ou x > 3
Sistemas de equações
1º Grau:
![]()
Vamos somar as duas equações; membro a membro:
![]()
3x = 18
x = 6
Substituindo numa das equações: 6 + y = 8
y = 2 Este é o método da Adição.
Veja agora o método da substituição:
![]()
1º) Vamos isolar y na 2ª Equação: y = 6 - x
2º) E substituir na 1ª: x2 - (6 - x)2 = 24
3º) Agora resolvendo...
x2 - (36 - 12x + x2) = 24
x2 - 36 + 12x - x2 = 24
12x = 60
x = 5
5 = x → y = 6 - x ⇒ y = 1
Inequações - Produto e Quociente
Observe o modelo:
![]()
1) Estudando o sinal de cada fator. 1- x = 0 ⇔ x = 1
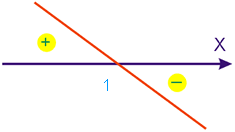
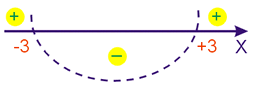
x² - 9 = 0 ⇔ x = 3 ou x = -3
2x - 8 = 0
x = 4
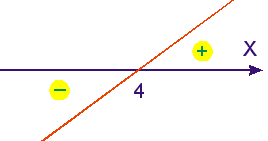
2) Agora vamos colocar estes dados no quadro de sinais.
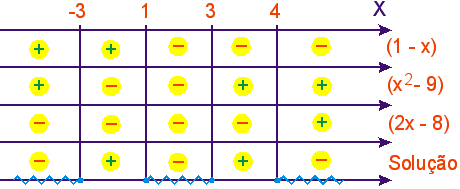
3) Como foi pedido negativo:
Temos
![]()
Sumário
- Equação do Primeiro Grau- Inequação do Primeiro Grau
- Conceito de desigualdade
- Equação do Segundo Grau
- Inequação do Segundo Grau
- Sistemas de equações
- Inequações - Produto e Quociente
Áreas exclusivas para assinantes





