Polias

ΔsPolias

Polia fixa

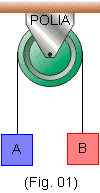
Na Fig. 1 representamos dois corpos A e B ligados por um fio ideal que passa por uma polia que pode girar sem atrito em torno de um eixo preso ao teto. Vamos supor que a massa da polia seja desprezível (polia ideal).

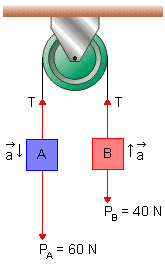
Na Fig. 2, P_A e P_B são as intensidades dos pesos de A e B. Entre o corpo A e o fio há um par de forças de intensidade T e entre o corpo B e o fio também há um par de forças de intensidade T.

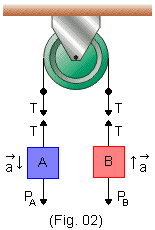
Supondo que P_A > P_B, se abandonarmos o sistema em repouso, a tendência será A descer e B subir, isto é,

P_A > T

e T > P_B

Assim, aplicando a segunda lei de Newton aos blocos obtemos:

PA - T = mA . a T - PB = mB . a

onde a é o módulo da aceleração de cada bloco. Resolvendo o sistema formado pelas duas equações obtemos os valores de a e T.

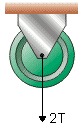
Observando a Fig. 2 percebemos que a força exercida sobre o eixo da polia tem intensidade 2T (Fig. 3).

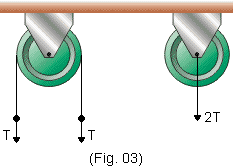
Exemplo 1

No sistema representado ao lado o fio e a polia são ideais. São dados:

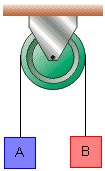
g = 10 m/s², m_A = 6,0 kg e m_B = 4,0 kg. Abandonando-se o sistema em repouso, calcule:

a) O módulo da aceleração dos blocos

b) O módulo da tração no fio

c) O módulo da força exercida pelo fio sobre a polia

Resolução

a)
	mA = 6,0 kg mB = 4,0 kg g = 10 m/s2		→		PA = mA . g = (6,0 kg) (10 m/s2) = 60 N PB = mB . g = (4,0 kg) (10 m/s2) = 40 N

Sendo P_A > P_B teremos:

P_A > T

e T > P_B

Apliquemos a segunda lei de Newton aos corpos A e B:

corpo A  P_A - T = m_A . a

corpo B  T - P_B = m_B . a

Substituindo os valores das massas e dos pesos temos:

60 - T = (6,0) . a (I) T - 40 = (4,0) . a (II)

Fazendo a soma membro das equações temos:

60 - 40 = 10 . a

a = 2,0 m/s²

b) Para calcular o valor de T substituímos o valor de a na equação I ou na equação II. Vamos fazer a substituição na equação II:

T - 40 = (4,0) . a

                        ↓

T - 40 = (4,0) . (2,0)

T - 40 = 8

T = 48 N

c) A força exercida pelo fio sobre a polia tem intensidade 2 T:

2 T = 2 (48) = 96 N

2T = 96 N

Exemplo 2

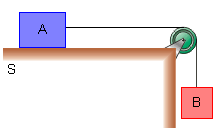
No sistema representado a seguir, os corpos A e B têm massas m_A = 16 kg e m_B = 4,0 kg. O fio e a polia são ideais e não há atrito entre o corpo A e a superfície S. Adotando g = 10 m/s² e abandonando-se o sistema em repouso, calcule:

A) A aceleração dos blocos

B) O módulo da tração no fio

C) O módulo da força exercida pelo fio sobre a polia.

Resolução

a) Neste caso, o peso de A(_A) é cancelado pela força normal (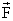_N)

P_B = m_B . g = (4,0 kg) (10 m/s²) = 40 N

Apliquemos a segunda lei de Newton aos corpos A e B:

corpo A → T = m_A . a  T = 16 . a (I)

corpo B → P_B - T = m_B . a  40 - T = (4,0). a (II)

Efetuando a soma membro a membro das equações I e II temos:

40 = 20 . a

a = 2,0 m/s²

b) Substituindo o valor de a na equação I temos:

T = 16 . a = 16 (2,0) = 32 N

T = 32 N

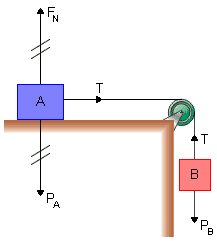
c) Na figura a seguir representamos as forças entre os blocos e o fio.

F é a intensidade da força exercida pelo fio sobre a polia.

Polia móvel

Na Fig. 4 representamos um sistema onde há duas polias. A polia α é fixa, isto é, o seu eixo é fixo; ela pode apenas girar em torno do seu eixo. Já a polia β é móvel; ela pode subir ou descer dependendo dos valores das massas de A e de B.

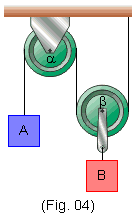
As forças exercidas nos blocos e nos fios estão representadas na Fig. 5. Suporemos que os fios e as polias são ideais.

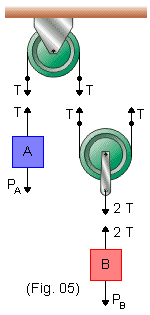
Pelo fato de o bloco B estar ligado ao eixo da polia B, a força "para cima" que atua sobre B, tem intensidade 2T

Condição de equilíbrio

Suponhamos inicialmente, que o sistema esteja em equilíbrio, isto é, ele está em repouso ou em movimento uniforme.

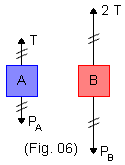
Observando a Fig. 6, percebemos que:

Equilíbrio de A → PA = T Equilíbrio de B → PB = 2T

Portanto:

P_B = 2T = 2P_A

P_B = 2P_A

m_Bg = 2m_Ag

m_B = 2m_A

Vemos então que um sistema formado por uma polia fixa e uma polia móvel é útil para suspender objetos (Fig. 7).

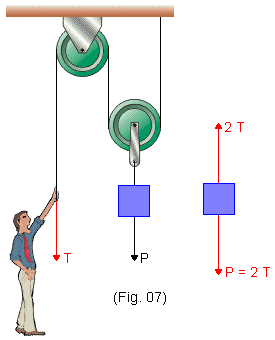
Na fig. 7 quando o indivíduo aplica ao fio uma força de intensidade T, consegue manter suspenso um corpo de peso 2 T. Esse é o princípio de funcionamento dos guindastes.

Sistema com aceleração

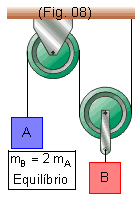
Vimos que, se m_B = 2 m_A o sistema estará em equilíbrio (Fig. 8). Assim,

I. Se m_B > 2 m_A, o bloco B terá aceleração para baixo e o bloco A terá aceleração   para cima (Fig. 9).

II. Se m_B < 2 m_A, o bloco B terá aceleração   para cima e o bloco A terá aceleração   para baixo (Fig. 10).

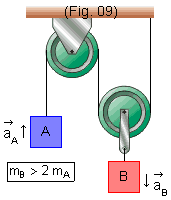
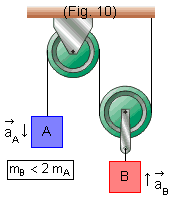
Quando os blocos tiverem aceleração, elas não serão iguais; como veremos a seguir, teremos:

a_A = 2 a_B

Para percebemos isso analisemos as figuras 11 e 12.

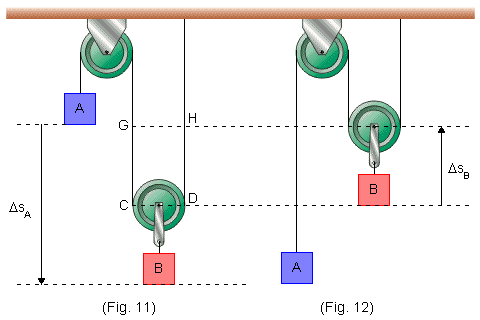
Suponhamos que, inicialmente o sistema esteja na posição da Fig. 11 e que após um intervalo de tempo Δt esteja na posição da Fig. 12. O bloco A percorreu um espaço Δs_A e o bloco B percorreu um espaço Δs_B. Observando a figura vemos que:

		__ GC		__ HD (I)
ΔsB	=		=

por outro lado, devemos ter:

		__ GC		__ HD (II)
ΔsA	=		+

Substituindo I em II:

		__ GC		__ HD
ΔsA	=		+

Δs_A = Δs_B + Δs_B

Δs_A = 2(Δs_B)  (III)

A igualdade III vale para qualquer intervalo de tempo. Portanto, podemos escrever:

v_A = 2 v_B (IV)

onde v_A é a velocidade A e v_B é a velocidade de B. Pode-se demostrar que a relação IV acarreta:

aA = 2 aB

Exemplo 3

No sistema representado abaixo as massas de A e B são m_A = 6,0 kg e m_B = 16 kg. Supondo g = 10 m/s². Calcule as acelerações dos blocos e a tração no fio.

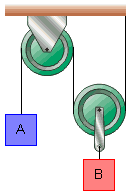
Resolução

Aqui temos:

m_B > 2 m_A

isto é: 16 > 2 (6,0)

Portanto, a aceleração de B () é para baixo e a aceleração de A () é para cima (Fig. 13).

    

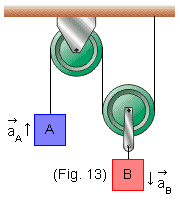
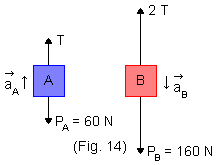
Isto significa que (Fig. 14):

T > PA PB > 2T

Apliquemos a segunda lei de Newton aos blocos (Fig. 14):

bloco A → T - PA = mA . aA bloco B → PB - 2T = mB . aB

Substituindo os valores conhecidos:

T - 60 = (6,0) . aA  (I) 160 - 2T = 16 . aB  (II)

Mas, sabemos que : a_A = 2 a_B. Substituindo na equação I:

T - 60 = 6,0 (2a_B) = 12a_B  (III)

Temos então o sistema formado pelas equações III e II:

T - 60 = 12 . aB  (III) 160 - 2T = 16 . aB  (II)

Dividindo os termos da equação II por 2 obtemos

T - 60 = 12 . aB  (III) 80 - T = 8 . aB  (IV)

Somando membro a membro:

80 - 60 = 20 a_B

20 = 20 a_B

a_B = 1,0 m/s²

Como a_A = 2 a_B temos:

a_A = 2,0 m/s²

Substituindo o valor de a_B na equação III:

T - 60 = 12 . a_B

T - 60 = 12 .(1,0)

T = 72 N