Queda Livre e Lançamento Vertical
- Home
- Queda Livre E Lançamento Vertical
Movimento Vertical No Vácuo - Mecânica
Consideremos um corpo em movimento vertical nas proximidades da superfície da Terra sob a ação de uma única força que é a sua força peso; estamos, portanto, supondo que não há resistência do ar, isto é, estamos supondo que o movimento se dá no vácuo. A experiência mostra que esse movimento tem uma aceleração aproximadamente constante, cujo módulo chama-se aceleração da gravidade e é representado por g. O valor de g não depende do tamanho, forma ou massa do corpo.
O valor de g varia de ponto a ponto da Terra, mas o seu valor é próximo de 9,8 m/s².
Como a queda livre é um movimento de aceleração constante, trata-se de um movimento uniformemente variado e, assim podemos usar as equações do MUV:
![]()
v = v0 + at
v2 = v02 + 2a(s - s0)
onde |a| = g. O sinal de a dependerá do eixo adotado como veremos adiante.
Para estudarmos esse movimento usamos as equações do M.U.V. tomando o seguinte cuidado:
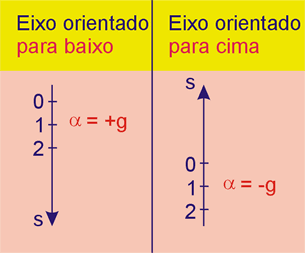
a) Se o eixo dos espaços for orientado para baixo, a aceleração é positiva: α = + g
b) Se o eixo for orientado para cima, a aceleração é negativa: α = - g
Exemplo 1
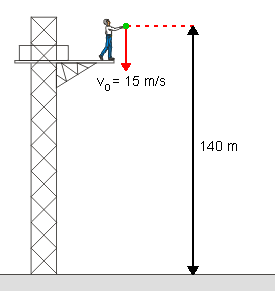
Numa região em que g = 10 m/s2, uma partícula é lançada para baixo, de uma altura de 140 metros, com velocidade inicial v0 = 15 m/s. Depois de quanto tempo a partícula atinge o solo? (despreze a resistência do ar)
Resolução
Adotado o eixo mostrado na figura abaixo temos:
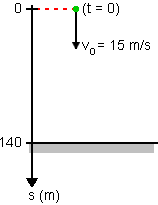
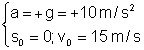
Assim, a equação horária do espaço é:
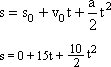
s = 15 + 5t2
Quando a partícula atingir o solo teremos s = 140 m:
140 =15t + 5t2
Simplificando ficamos com a equação
t2 + 3 t - 28 = 0
As raízes dessa equação são
t = 4 e t = -7
Desprezamos a resposta negativa e ficamos com a resposta positiva:
t = 4 s
LANÇAMENTO PARA CIMA
Na Fig. 1 representamos uma situação em que uma partícula é lançada verticalmente para cima, saindo da mão da pessoa com velocidade inicial v0 . Neste caso, durante a subida o movimento é retardado o módulo da velocidade vai diminuindo até atingir a altura máxima (ponto B) onde a velocidade é nula. A seguir a partícula começa a descer com movimento acelerado: durante a descida o módulo da velocidade vai aumentando.
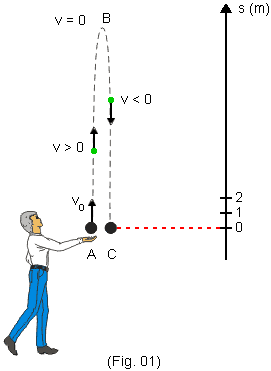
Para facilitar a análise vamos supor v0 = 30 m/s e g = 10 m/s.
No caso em que o lançamento é para cima é mais prático adotar um eixo orientado para cima (Fig. 1). Desse modo, na subida a velocidade é positiva pois o movimento é a favor do eixo. Porém, na descida, o movimento tem sentido oposto ao do eixo e, assim, na descida a velocidade é negativa.
|
t (s)
|
v (m/s)
|
|
0
|
30
|
|
1
|
20
|
|
2
|
10
|
|
3
|
0
|
|
4
|
-10
|
|
5
|
-20
|
|
6
|
-30
|
Como g = 10 m/s2 , isto significa que, a cada segundo, o módulo da velocidade varia de 10 m/s; na subida o módulo diminui e na descida o módulo aumenta. Acrescentando os sinais obtemos a tabela abaixo. Do ponto de vista algébrico, a cada segundo há uma diminuição de 10 m/s. Portanto, neste caso a aceleração é negativa tanto na subida como na descida:
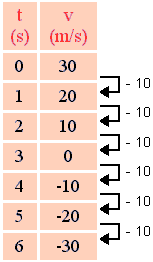
a = -g = -10 m/s2
Percebemos então que, no momento de usar as equações do MUV, o sinal da aceleração vai depender do eixo adotado:
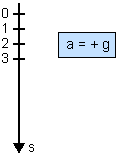
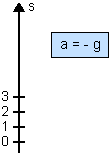
Exemplo 2
Da janela de um edifício, um garoto lança verticalmente para cima uma bola, com velocidade inicial 10 m/s. No momento do lançamento a bola está a 75 metros de altura, como ilustra a figura.
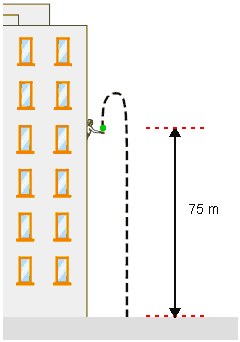
Adotando g = 10 m/s2 e desprezando a resistência do ar pede-se:
a) depois de quanto tempo a bola atinge a altura máxima?
b) depois de quanto tempo a bola atinge o solo?
c) Esboce o gráfico do espaço em função do tempo.
Resolução
a) Adotando um eixo orientado para cima cuja origem está no solo (Fig. 6), temos:
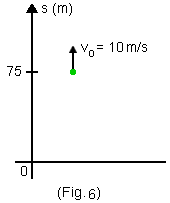
| = 75m; v0 = 10 m/s = -g = -10m/s2 |
A equação horária da velocidade escalar é:
v = v0 + a t
v = 10 - 10 t
A bola atinge a altura máxima no instante em que v = 0:
| v | = 10 - 10t | |
| 0 | = 10 - 10t | |
t = 1s
b) A equação horária do espaço é:
| s = s0 + v0t + | a/2 | t2 |
| s = 75 + 10t + | (-10)/2 | t2 |
s = 75 + 10t-5t2
Quando a bola atingir o solo teremos s = 0:
| s | = 75 +10t - 5t2 |
| ↓ | |
| 0 | = 75 +10t - 5t2 |
Simplificadamente obtemos: t2 - 2 t - 15 = 0
As raízes dessa equação são e 5 e -3. Considerando apenas a raiz positiva temos
t = 5s
c) Considerando a equação horária do espaço, vamos colocar alguns valores no lugar de t:
s = 75 + 10t - 5t2
t = 0 ⇒ s = 75 + 10 (0) - 5 (0)2 = 75
t = 1 ⇒ s = 75 + 10 (1) - 5 (1)2 = 80
t = 2 ⇒ s = 75 + 10 (2) - 5 (2)2 = 75
t = 3 ⇒ s = 75 + 10 (3) - 5 (3)2 = 60
t = 4 ⇒ s = 75 + 10 (4) - 5 (4)2 = 35
t = 5 ⇒ s = 75 + 10 (5) - 5 (5)2 = 0
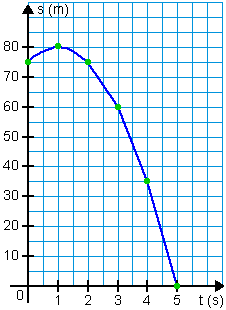
A bola gasta 1 segundo para atingir a altura máxima (80 m) e mais 1 segundo para voltar à altura inicial (75 m). O tempo total de descida é igual a 4 segundos (desde t = 1 s até t = 5 s).
Sumário
- Movimento Vertical no Vácuo- Lançamento para Cima
Áreas exclusivas para assinantes





