Atrito Estático - Atrito Cinético
- Home
- Atrito Estático Atrito Cinético
Força de Atrito - Atrito Estático - Atrito Cinético
Quando não há deslizamento entre as superfícies, a força de atrito chama-se estática.
Quando existe deslizamento entre as superfícies a força de atrito chama-se cinética (ou dinâmica).
É importante também ressaltar que nem sempre a força de atrito é oposta ao movimento.
Atrito Estático
A força de atrito que impede um corpo de se movimentar, em relação ao plano de apoio é chamada força de atrito estática ( ![]() ).
).

![]()
Como a intensidade da força de atrito depende da intensidade da força ![]() aplicada no bloco (vide figura acima), o seu valor não é fixo, podendo variar de zero a um valor máximo. Porém, a experiência mostra que a força de atrito não aumenta indefinidamente, isto é, se o indivíduo aplicar uma força suficientemente intensa, conseguirá tirar o bloco do repouso. Portanto, existe um valor máximo para a força de atrito, chamada de força máxima de atrito (
aplicada no bloco (vide figura acima), o seu valor não é fixo, podendo variar de zero a um valor máximo. Porém, a experiência mostra que a força de atrito não aumenta indefinidamente, isto é, se o indivíduo aplicar uma força suficientemente intensa, conseguirá tirar o bloco do repouso. Portanto, existe um valor máximo para a força de atrito, chamada de força máxima de atrito (![]() ).
).
A força máxima de atrito é dada por:
![]() =
= ![]() . Fn
. Fn
onde Fn é a intensidade da força normal e μe é um coeficiente chamado coeficiente de atrito estático o qual depende dos materiais em contato (e do estado de polimento).
Exemplo 1
Um bloco de massa m = 2,0 kg está inicialmente em repouso sobre uma superfície horizontal S. A partir de certo instante aplicamos ao corpo uma força horizontal de intensidade F = 16 N. Sabe-se que g = 10 m/s2 e que o coeficiente de atrito cinético entre bloco e a superfície é μc = 0,30.
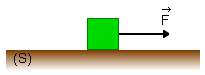
Calcule:
A intensidade da força de atrito que atua sobre o bloco
Resolução
Na figura abaixo marcamos todas as forças que atuam sobre o bloco: a força ![]() , a força de atrito
, a força de atrito ![]() , o peso
, o peso ![]() e a força normal
e a força normal ![]() .
.
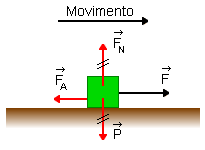
P = mg = (2,0 kg) (10 m/s2) = 20 N
Neste caso a força normal tem a mesma intensidade que o peso;
FN = P = 20 N
A intensidade da força de atrito é dada por:
FA = μc.FN = (0,30) (20) = 6,0 N
FA = 6,0 N
Atrito Cinético
A força de atrito que é aplicada num corpo, no sentido oposto ao seu movimento, pelo plano de apoio, é chamada força de atrito cinética e sua intensidade, que também depende da compressão normal.
A experiência mostra que o módulo da força de atrito cinético 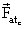 é dada por:
é dada por:
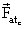 = μc . Fn
= μc . Fn
onde FN é a intensidade da força normal atuante no corpo e ![]() é um número chamado coeficiente de atrito cinético, o qual depende dos materiais do corpo e das superfícies de contato; esse coeficiente depende também do estado de polimento das superfícies em contato.
é um número chamado coeficiente de atrito cinético, o qual depende dos materiais do corpo e das superfícies de contato; esse coeficiente depende também do estado de polimento das superfícies em contato.
Exemplo 2
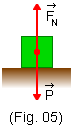
Um bloco de massa m = 6,0 kg está inicialmente em repouso sobre uma superfície horizontal S, sob a ação de apenas duas forças (Fig. 5): o peso ![]() e a força normal. A partir de certo instante aplicamos ao bloco uma força horizontal
e a força normal. A partir de certo instante aplicamos ao bloco uma força horizontal ![]() e ao mesmo tempo aparece uma força de atrito
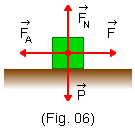
e ao mesmo tempo aparece uma força de atrito ![]() (Fig. 6). Os coeficientes de atrito para este caso são:
(Fig. 6). Os coeficientes de atrito para este caso são:
μe = 0,30 e μc= 0,20
Sabendo que g = 10 m/s2, calcule a intensidade da força de atrito, nos seguintes casos:
a) F = 12 N
b) F = 18 N
Resolução
a) A intensidade F = 12 N ainda é menor do que 18 N. Portanto, o bloco continua em repouso e, assim, a força de atrito tem a mesma intensidade que a força aplicada F (Fig. 8):
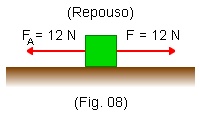
FA = 12 N
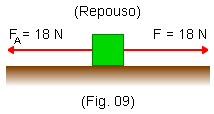
b) Neste caso a força aplicada (![]() ) tem a mesma intensidade que a força de atrito máxima (18 N). Assim, o bloco continua em repouso e a força de atrito está com seu valor máximo (Fig. 9). Dizemos que o bloco está na iminência de movimento.
) tem a mesma intensidade que a força de atrito máxima (18 N). Assim, o bloco continua em repouso e a força de atrito está com seu valor máximo (Fig. 9). Dizemos que o bloco está na iminência de movimento.
Sumário
- Atrito Estático- Atrito Cinético
Áreas exclusivas para assinantes





