Cinemática Escalar

Mecânica - Cinemática

A velocidade e a aceleração são grandezas vetoriais. Porém, em certos casos podemos esquecer esse caráter vetorial e interpretar tanto a velocidade como a aceleração, como sendo grandezas escalares; esses casos são tratados pela Cinemática Escalar que estudaremos a seguir. Mais tarde estudaremos a Cinemática Vetorial, isto é, aqueles casos em que é necessário considerar o caráter vetorial da velocidade e da aceleração.

Ponto Material

Chamamos de ponto material, um objeto cujo tamanho e estrutura interna não são importantes para o problema com que lidamos, além de não nos interessarmos por eventuais rotações, isto é, estamos interessados apenas na sua translação. A Terra, por exemplo, pode ser olhada como um ponto material para a maioria dos problemas de movimento planetário, mas certamente não para problemas terrestres. Frequentemente usaremos a palavra partícula no lugar de ponto material.

Sistemas de Referência

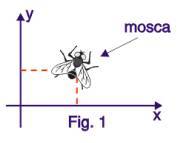
Chamamos de sistema rígido, todo sistema de pontos para o qual a distância entre dois pontos quaisquer permanece invariável. Em outras palavras, sistema rígido é um sistema indeformável. Podemos determinar a posição de um ponto, dando suas distâncias aos pontos do sistema rígido. No caso de o sistema rígido ser usado para determinar posição, dizemos que ele constitui um sistema de referência, ou simplesmente referencial. Por exemplo, se tivermos uma mosca andando sobre uma mesa, podemos usar como sistema rígido, para determinar sua posição, um par de eixos perpendiculares (figura 1) e determinar sua posição dando as coordenadas cartesianas da mosca.

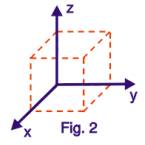
Porém, nem todos os movimentos vão se dar apenas num plano, mas sim, poderão ser espaciais. Nesse caso, o tipo mais usado de sistema rígido é um conjunto de 3 eixos perpendiculares entre si que passam por um mesmo ponto (figura 2).

Movimento e repouso

Suponha que você está viajando em um trem; suponha ainda que você esteja conversando com um amigo (que se encontra parado em uma das estações, por exemplo) através de um rádio transmissor, e que em dado momento ele pergunte a você se a lâmpada do teto do vagão está em repouso ou em movimento. Se você respondesse que a lâmpada está em repouso, um indivíduo no chão, fora do vagão, poderia dizer que a lâmpada está em movimento e nenhum dos dois estaria errado.

Esse exemplo mostra que movimento e repouso são conceitos relativos, isto é, não podemos dizer simplesmente que tal objeto está parado ou está se movimentando, mas sim, devemos especificar, em relação a que referencial o objeto está em repouso. No caso do trem, as afirmações corretas seriam:

• a lâmpada está em repouso, em relação a um observador situado no trem.
• a lâmpada está em movimento, em relação a um observador fixo em relação ao solo.

Dizemos então, que um certo ponto encontra-se em movimento em relação a um certo referencial, se pelo menos uma das coordenadas do ponto variar com o tempo.

Dizemos que um ponto está em repouso em relação a um certo referencial, se nenhuma de suas coordenadas variar com o tempo.

Trajetória

Consideremos os pontos ocupados por um móvel com o correr do tempo, em relação a um dado referencial. Unamos os pontos obtendo assim uma linha, a qual chamaremos de trajetória do móvel em relação ao referencial adotado.

Por essa definição podemos concluir, que a forma da trajetória dependerá do referencial adotado. Por exemplo, consideremos um avião que solta uma granada (figura 3).

Um indivíduo no chão observará uma trajetória curva, enquanto que o indivíduo que soltou a granada observará uma trajetória reta e vertical, isto é, seria a mesma trajetória que ele notaria se soltasse a granada do alto do Edifício Itália (Desprezando a resistência do ar).

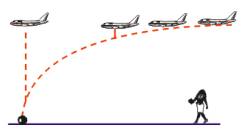(Fig. 3)

Posição escalar

Vamos iniciar agora, realmente, a cinemática escalar. Vamos escolher um referencial, e em relação a esse referencial, vamos considerar a trajetória do móvel em estudo e vamos fazer com essa trajetória o mesmo que foi feito em geometria analítica com a reta. Vamos marcar uma origem, considerar um sentido como positivo e colocar as "marcas" nessa estrada (figura 4).

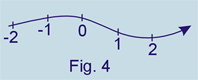
Nas estradas de rodagem, os marcos são colocados de quilômetro em quilômetro, mas na nossa trajetória, poderemos colocar de metro em metro, de centímetro em centímetro ou mesmo de polegada em polegada.

Em geometria analítica a posição de um ponto é determinada pela sua abscissa. Por exemplo, na figura 5, a abscissa do ponto A é +2 e a abscissa do ponto B é -3.

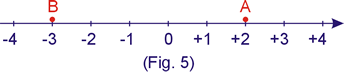
Na cinemática faremos o mesmo, porém usando a palavra "espaço" no lugar de "abscissa"; além disso devemos informar também a unidade usada.  Assim, por exemplo, na figura 6 temos uma trajetória "graduada" em quilômetros; o espaço do ponto M é 3 km e indicamos por:

s_M = 3 km 

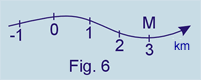
O espaço também é chamado de posição escalar.

Movimentos Progressivos e Retrógrados

Quando o movimento de uma partícula se dá no sentido dos espaços crescentes dizemos que o movimento é progressivo; se o movimento se dá no sentido dos espaços decrescentes o movimento é dito retrógrado.

(Fig 7)

Deslocamento escalar ou Variação do espaço (Δs)

Sendo s_a e s_b os espaços de uma partícula nos instantes t_a e t_b respectivamente (com t_b > t_a) , chamamos de variação de espaço entre os instantes t_a e t_b ( representado por Δs) a diferença s_b - s_a:

Generalizando

 , onde:

s_f = posição escalar final

s_i = posição escalar inicial

Observações:

I - Quando um movimento é progressivo Δs > 0

II - Quando um movimento é retrógrado Δs < 0

Distância percorrida (d)

Quando o movimento é sempre progressivo ou sempre retrógrado temos:

Quando o movimento é composto de várias etapas

Velocidade Escalar Média (v_m)

Consideremos uma partícula que no instante t_A tem espaço s_A e no instante t_{B >} t_A tem espaço s_B.  A velocidade escalar média entre os instantes t_A e t_B é definida por:

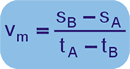
Generalizando:

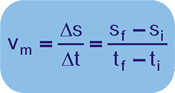
Observações:

I - Quanto um movimento é sempre progressivo temos v_m > 0

II - Quando um movimento é sempre retrógrado temos v_m < 0

Velocidade Escalar Instantânea (v)

A velocidade escalar média é calculada entre dois instantes; além dessa velocidade podemos definir a velocidade escalar instantânea que, como o próprio nome diz, é a velocidade escalar num determinado instante. No entanto, para definir esta velocidade precisamos de uma "ferramenta" matemática que está fora do vestibular: é a teoria dos Limites e Derivados. Assim sendo apresentaremos a definição apenas por curiosidade, mas não vamos utilizá-la:

a velocidade escalar instantânea (v) é definida por:

Isto significa que para calcularmos a velocidade escalar instantânea, calculamos a velocidade escalar média   num intervalo de tempo "tendendo a zero".  Como nós não poderemos fazer esse cálculo, encararemos o conceito de velocidade escalar instantânea como um conceito "intuitivo". A "grosso modo", a velocidade escalar instantânea é o que marca o velocímetro do automóvel.

De modo geral, a velocidade escalar média (v_m) e a velocidade escalar instantânea (v) são conceitos diferentes. Mas, se durante um movimento, o valor de v  ficar constante, então:

V­­_m = V

Para velocidade escalar instantânea valem duas propriedades idênticas a duas que foram apresentadas para a velocidade escalar média:

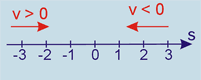
1ª) Se num determinado instante o movimento é progressivo, então v > 0

2ª) Se num determinado instante o movimento é retrógrado, então v < 0.

Observação:

Quando escrevemos "velocidade escalar" sem especificar se é média ou instantânea, por convenção estamos nos referindo à velocidade escalar  instantânea.

Avalie a aula