Trabalho e Potência

Trabalho e Potência

TRABALHO REALIZADO POR UMA FORÇA CONSTANTE

Consideremos um corpo que, sob a ação de uma força constante efetua um deslocamento (Fig. 1). 

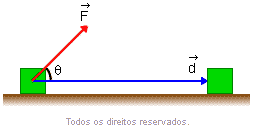
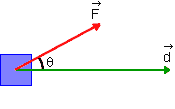
O trabalho da força ao longo desse deslocamento é definido por:

τ = F.d..cos θ

onde θ é o ângulo formado entr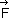e   e  .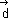

No sistema Internacional a unidade de trabalho é o joule (J).

Diagrama Força Tangencial x Deslocamento

Esta propriedade permite o cálculo do trabalho realizado por forças constantes e variáveis. Neste gráfico a força é analisada do ponto de vista escalar.

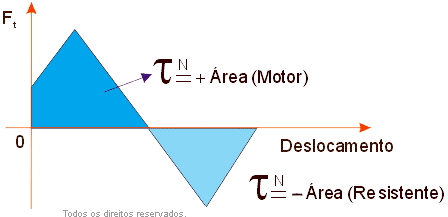
O trabalho é positivo quando a força é a favor do movimento (Trabalho motor)

O trabalho é negativo quando a força é contra o movimento (Trabalho resistente)

Trabalho Realizado Pela Força Peso (_p)

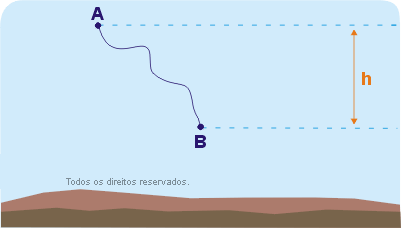
Qualquer que seja a trajetória entre os pontos A e B, tem-se que:

onde g é a aceleração da gravidade e h é o desnível entre os pontos A e B.

Se o ponto final estiver abaixo do ponto inicial, isto é, o corpo desceu, o trabalho é positivo. Se o ponto final estiver acima do ponto inicial, isto é, o corpo subiu, o trabalho é negativo.

de A para B (desce): _{p > 0}

de B para A (sobe): _{p < 0}

Trabalho de uma força centrípeta

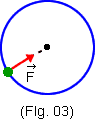
Consideremos agora o caso de um corpo em movimento circular. Nesse caso, sabemos que deve haver uma força apontando para o centro da trajetória. (Fig. 3).

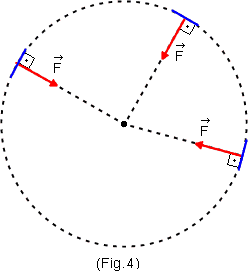
Para calcular o trabalho de  devemos dividir a trajetória em pequenos pedaços (Fig. 4) e calcular o trabalho em cada pedaço. Mas, em cada pedaço a força é perpendicular ao deslocamento e assim, em cada pedaço o trabalho é nulo. Portanto o trabalho de  é nulo:

Potência

Quando uma força está realizando trabalho, às vezes estaremos interessados em saber a rapidez com que esse trabalho está sendo feito. Para medir essa rapidez, definimos a Potência Média (P_m) da força por:

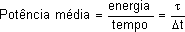
onde 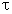é o trabalho realizado num intervalo de tempo Δt. No Sistema Internacional de Unidades a potência é expressa em watts (W).

Potência e velocidade

Consideremos uma força constante atuando num corpo em um deslocamento , durante um intervalo de tempo Δt (Fig.1). A potência média de nesse intervalo de tempo será:

Para 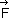constante :

P_m = F . V_m . cos θ

Quando a força é paralela ao deslocamento

P = F . V

Outras unidades de potência:

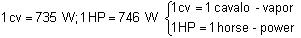
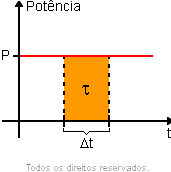
Diagrama Potência x Tempo

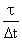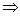P =		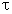=	P . (Δt)
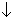			área

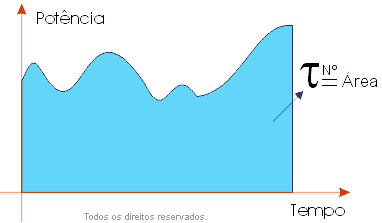
Essa propriedade permite o cálculo do trabalho realizado por forças constantes e variáveis.

Potência constante	Potência variável

Potência e energia

O conceito de potência aplica-se também quando um corpo está recebendo ou fornecendo energia.

Suponhamos que, num certo intervalo de tempo Δt, um corpo receba (ou forneça) uma energia E. A potência média recebida (ou fornecida) nesse intervalo de tempo é:

Como a unidade de energia é igual à unidade de trabalho, também nesse caso, a unidade de potência é o watt (ou Hp ou cv).

Continua valendo também a propriedade da área. Num gráfico da potência recebida (ou fornecida) por um corpo, em função do tempo (Fig.5) a área da figura sombreada é numericamente igual à energia recebida (ou fornecida) pelo corpo, no intervalo de tempo .

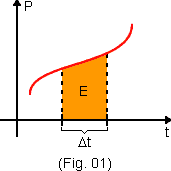
A energia E pode ser uma energia mecânica mas poder também ser um outro tipo de energia como por exemplo, a energia elétrica ou o calor.

Avalie a aula