Sistemas Lineares
- Home
- Sistemas Lineares
Sistemas Lineares
Um conjunto com m (m ≥ 1) equações lineares a n incógnitas x1, x2, x3,.... xn denomina-se sistema linear.
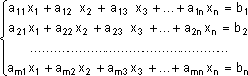
Se o conjunto ordenado de números (α1, α2, α3,.... αn) satisfazer todas as equações lineares do sistema, será denominado solução do sistema linear.
Exemplo
![]() tem como solução x = 1 e y = 3, ou seja, (1 ; 3).
tem como solução x = 1 e y = 3, ou seja, (1 ; 3).
Classificação
Os sistemas lineares são classificados quanto ao número de soluções da seguinte maneira:

Exemplo
![]() não tem solução
não tem solução
![]() tem solução indeterminada que pode ser representada por
tem solução indeterminada que pode ser representada por ![]()
Expressão matricial de um sistema linear
Chamamos de D o determinante da matriz dos coeficientes das incógnitas, isto é,
D = 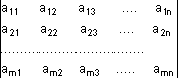
Regra de Cramer
Esta regra só poderá ser usada para sistemas possíveis e determinados.
Um sistema linear será SPD se D ≠ 0 e neste caso as soluções serão dadas por:
![]()
Onde D1, D 2, D3,.... Dn são os determinantes que se obtém da matriz dos coeficientes das incógnitas, substituindo-se a coluna dos coeficientes da incógnita procurada pelos termos independentes b 1, b2,.... bn.
Exemplo
Resolver o sistema linear utilizando a regra de Cramer
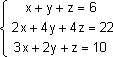
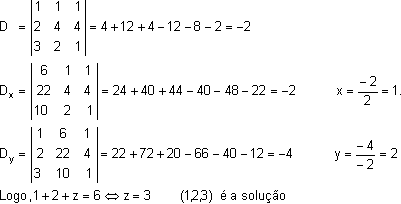
Sistema Escalonado
Sistema lineares são ditos equivalentes se possuem o mesmo conjunto solução.
Sistemas escalonados são aqueles que apresentam zeros (0), como coeficientes das variáveis da seguinte forma:
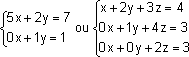
Propriedades Operacionais para Obtermos um Sistema Escalonado
Propriedade 1: Num sistema linear quando trocarmos as posições de duas equações o sistema é equivalente ao anterior
Propriedade 2: Num sistema linear, ao se multiplicar uma equação por um número real não nulo, o sistema continua equivalente.
Propriedade 3: Num sistema linear, ao se multiplicar uma equação por um número real (não nulo) e somando-se esta a uma outra equação, o sistema obtido é equivalente ao anterior.
Discussão de um Sistema Linear
Discutir um sistema quer dizer verificar se o sistema é possível, impossível ou indeterminado.
SPD se D ≠ 0
SPI se D = 0 e D1 = D2 = ...Dn = 0
SI se D = 0 e pelo menos um Di ≠ 0
Exemplo
Dado:
![]()
discutir o sistema abaixo.
Seja:
![]() o determinante do sistema.
o determinante do sistema.
D = a2 - 6a = 0 ↔ a = 0 ou a = 6.
a = 0 ![]()
x = 2 e y é qualquer.
Logo o sistema é indeterminado.
a = 6 ![]()
Logo o sistema é impossível.
Resumindo: ![]()
a = 6 SI.
Sumário
- Classificação- Expressão matricial de um sistema linear
- Regra de Cramer
- Sistema Escalonado
- Propriedades Operacionais
- Discussão de um Sistema Linear
Áreas exclusivas para assinantes





