Potencial Elétrico
- Home
- Potencial Elétrico
Potencial Elétrico
Energia Potencial
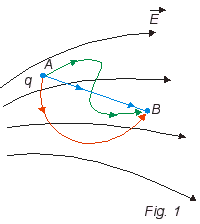
Consideremos uma região do espaço onde há um campo elétrico estático, isto é, que não varia no decorrer do tempo. Suponhamos que uma carga puntiforme q seja levada de um ponto A para um ponto B dessa região (Fig. 1). É possível demonstrar que o trabalho da força elétrica nesse percurso não depende da trajetória seguida, isto é, qualquer que seja a trajetória seguida, o trabalho da força elétrica entre A e B ![]() é o mesmo. Portanto a força elétrica é conservativa e podemos assim definir uma energia potencial.
é o mesmo. Portanto a força elétrica é conservativa e podemos assim definir uma energia potencial.
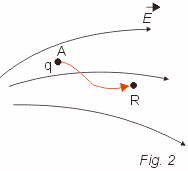
Como já vimos na mecânica, o valor exato da energia potencial não é importante. O que importa na realidade é a diferença da energia potencial no percurso. Portanto podemos escolher um ponto R qualquer como referencial, isto é, o ponto onde a energia potencial é considerada nula.
Escolhido o ponto R (Fig. 2), a energia potencial de uma carga q num ponto A ![]() é, por definição, igual ao trabalho da força elétrica quando a carga é levada de A até R:
é, por definição, igual ao trabalho da força elétrica quando a carga é levada de A até R:
![]()
Podemos definir também o potencial do ponto A (VA) como sendo a energia potencial por unidade de carga:
![]()
No Sistema Internacional a unidade de potencial é o volt (V):
![]()
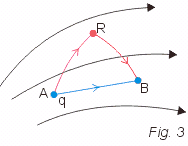
Suponhamos que uma carga puntiforme q seja levada de um ponto A para um ponto B (Fig. 3). Como a força elétrica é conservativa o trabalho não depende da trajetória. Portanto, podemos escolher uma trajetória que vá de A para R e de R para B:
![]()
mas: ![]()
Substituindo em III:
![]()
Porém: ![]()
Substituindo em IV:
![]()
isto é, o trabalho da força elétrica para ir de A até B é igual à diferença de energia potencial entre A e B.
Lembrando que:
![]()
e substituindo em V obtemos:
![]()
![]()
A diferença de potencial VA - VB costuma ser representada por UAB:
UAB = VA - VB
Propriedades do Potencial
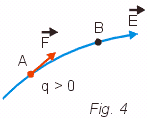
Consideremos uma carga puntiforme q positiva sendo levada de um ponto A para um ponto B sobre uma linha de força (Fig. 4). Como a carga é positiva, a força ![]() tem o mesmo sentido do campo e, desse modo, o trabalho da força elétrica será positivo
tem o mesmo sentido do campo e, desse modo, o trabalho da força elétrica será positivo ![]() .
.
Assim:
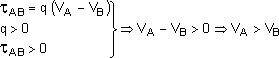
Percebemos então que o potencial do ponto A é maior que o potencial do ponto B. Portanto:
|
o potencial diminui ao longo de uma linha de força. |
Movimento espontâneo
Se abandonamos uma carga q numa região onde há campo elétrico, supondo que não haja nenhuma outra força, a carga deverá se deslocar "a favor" da força elétrica, isto é, a força elétrica realizará um trabalho positivo. Consideremos duas possibilidades: q > 0 e q < 0.
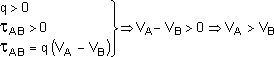
Percebemos então que:
|
uma carga positiva, abandonada numa região onde há campo elétrico, desloca-se espontaneamente para pontos de potenciais decrescentes. |
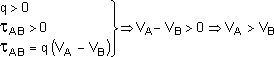
Portanto:
|
uma carga negativa abandonada numa região onde há campo elétrico, desloca-se espontaneamente para pontos de potenciais crescentes. |
Superfícies Equipotenciais
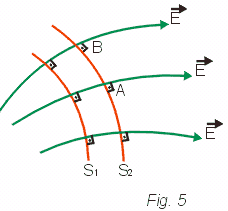
Na Fig. 5, as linhas S1 e S2 representam no espaço, superfícies que, em cada ponto, são perpendiculares à linhas de força. Suponhamos que uma carga q seja transportada de um ponto A para um ponto B, de modo que a trajetória esteja sobre uma dessas superfícies. Nesse caso, em cada pequeno trecho da trajetória, a força elétrica será perpendicular ao deslocamento e, portanto, o trabalho da força elétrica será nulo:
![]()
Concluímos então que todos os pontos dessa superfície têm o mesmo potencial e por isso ela é chamada de superfície equipotencial. Assim, na Fig. 5, S1 e S2 são exemplos de superfícies equipotenciais.
O Elétron - Volt
Na área de Física Nuclear é usada uma unidade de energia (ou trabalho) que não pertence ao Sistema Internacional: o elétron - volt (eV). Essa unidade é definida como sendo o módulo do trabalho realizado pela força elétrica quando um elétron é deslocado entre dois pontos cuja diferença de potencial é 1 volt. Lembrando que, em módulo, a carga de um elétron é 1,6 . 10-19 C temos:
![]()
![]()
1eV = 1 elétron - volt = 1,6 . 10-19J
Potencial e Campo Uniforme
Na Fig. 6 representamos algumas linhas de força de um campo elétrico uniforme ![]() . Como as superfícies equipotenciais devem ser perpendiculares às linhas de força, neste caso as superfícies equipotenciais são planos perpendiculares às linhas. Na Fig. 6, SA e SB representam duas superfícies equipotencial. Todos os pontos de SA têm um mesmo potencial VA e todos os pontos de SB têm um mesmo potencial VB.
. Como as superfícies equipotenciais devem ser perpendiculares às linhas de força, neste caso as superfícies equipotenciais são planos perpendiculares às linhas. Na Fig. 6, SA e SB representam duas superfícies equipotencial. Todos os pontos de SA têm um mesmo potencial VA e todos os pontos de SB têm um mesmo potencial VB.
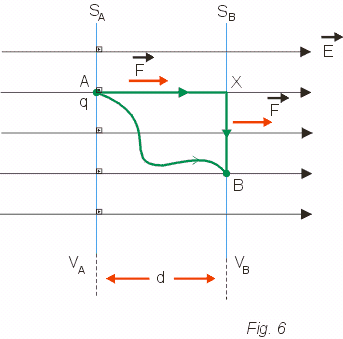
Suponhamos que uma carga positiva q seja transportada do ponto A para o ponto B. O trabalho da força elétrica não depende da trajetória. Portanto podemos fazer o percurso A X B indicado na figura:
![]()
No trecho XB a força elétrica é perpendicular ao deslocamento e, portanto, no trecho AX temos:
![]()
Substituindo em VII:
![]()
Mas sabemos que: ![]()
Assim: ![]()
UAB = E . d (VIII)
Como o potencial decresce ao longo de uma linha de força temos VA > VB. Portanto, se quiséssemos VB - VA teríamos:
VB - VA = UBA = - E . d
Unidade de E no SI
No capítulo anterior vimos que, no SI, a unidade do campo elétrico pode ser o newton por coulomb (N/C). No entanto a unidade oficial do campo elétrico no SI é outra, a qual pode ser obtida da equação VIII:
![]()
Assim:
![]()
Potencial e Campo de Carga Puntiforme
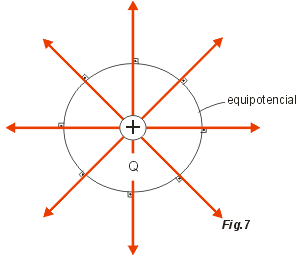
Quando o campo elétrico é produzido por uma única carga puntiforme Q, sabemos que as linhas de força são radiais como indicam as figuras 7 e 8.
 |
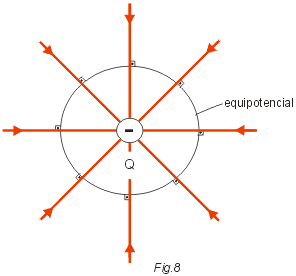 |
Como as superfícies equipotenciais devem ser perpendiculares às linhas de força, neste caso, as superfícies equipotenciais são superfícies esféricas cujo centro estão sobre a carga Q.
Suponhamos que a carga Q esteja fixa, e uma carga puntiforme q seja transportada de um ponto A para um ponto B. É possível mostrar que o trabalho da força elétrica neste caso é dada por:
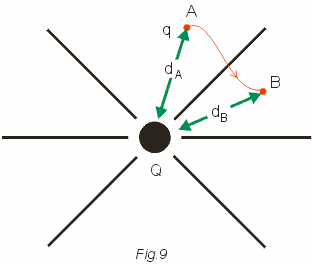
![]()

Portanto, a diferença de potencial entre os pontos A e B é dada por:
![]()
A partir da equação vemos que neste caso é conveniente adotar o referencial no infinito, pois para ![]() o termo
o termo ![]() . Assim, teremos:
. Assim, teremos:
![]()
ou, de modo geral:
![]()
Ainda supondo o referencial no infinito, da equação IX tiramos:
![]()
ou, de modo geral:
![]()
Sumário
- Energia Potencial
- Propriedades do Potencial
i. Movimento espontâneo
ii. Superfícies Equipotenciais
- O Elétron - Volt
- Potencial e Campo Uniforme
- Unidade de E no SI
- Potencial e Campo de Carga Puntiforme
Áreas exclusivas para assinantes





