Lançamento Horizontal e Oblíquo

Lançamento Oblíquo no Vácuo

No vácuo, ou em meios onde as resistências passivas podem ser desprezadas, o movimento de um projétil pode ser decomposto em duas direções:

- movimento horizontal - eixo x

- movimento vertical - eixo y

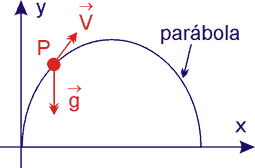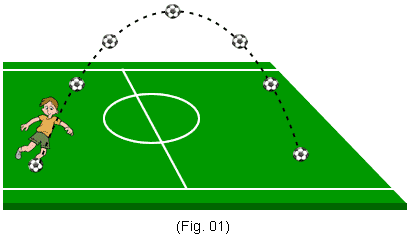
Na Fig.1 representamos um jogador chutando uma bola de futebol. A bola sai do pé do jogador com velocidade  que forma ângulo θ com a horizontal.

       

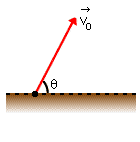
Após o lançamento, o peso, na vertical é a única força agente, considerando constante, temos:

Componentes da Velocidade Inicial

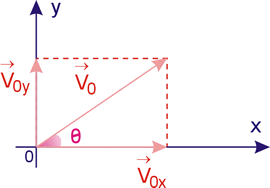
θ = ângulo de lançamento ("ângulo de tiro")

Da figura temos:

Movimento Componente Horizontal

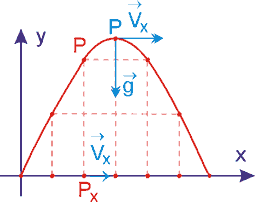
Na horizontal não há forças atuantes. Portanto:

I - O movimento é uniforme e retilíneo

II - A velocidade é constante, de módulo:

III - Sua equação horária é:

 

Movimento Componente Vertical

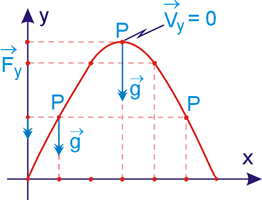
Na vertical atua a força peso, portanto:

I - O movimento é uniformemente variado, retilíneo

II - A aceleração escalar constante vale:

III - A equação de sua velocidade escalar (V_y) é:

IV - Sua equação horária é:

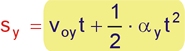 (equação de um M.U.V.) ou seja:

V - Vale também a equação de Torricelli:

Propriedades do Movimento

1. No pico da trajetória, a velocidade vetorial tem direção horizontal e valor mínimo, diferente de zero. A componente vertical é zero, nesse ponto.

2. O tempo total de subida é igual ao tempo de descida, e vale:

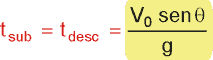   ( V_y = 0)

(fazendo Vy = 0 na equação de Torricelli)

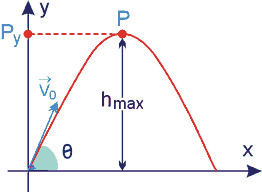
3. A altura máxima aumenta com o ângulo de tiro (fixados V_o e g) e vale:

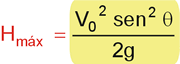   (fazendo V_y = 0 na equação de Torricelli)

4. O alcance horizontal, D, cresce com o ângulo de tiro, sendo máximo (D_máx) a 45º fixados V_o e y.

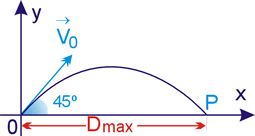
É útil lembrar que o alcance, independentemente do valor do ângulo de tiro, é obtido fazendo-se o tempo total igual a 2 vezes o tempo de subida.

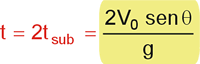
5. Em qualquer instante, a velocidade vetorial é dada por:

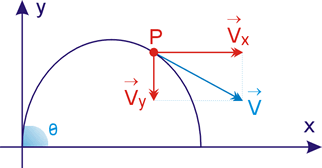
O módulo de  é dado por:

Lançamento Horizontal no vácuo

O lançamento horizontal pode ser encarado como sendo um caso particular de lançamento oblíquo.

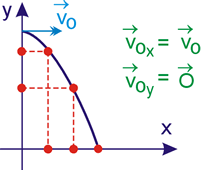
Na figura abaixo mostramos uma bola que rola sobre uma mesa e cai. Suponhamos que o experimento seja feito no vácuo, isto é, não haja resistência do ar. Nesse caso, sendo  a velocidade da bola no momento em que abandona a mesa, durante a queda a bola continua a ir para a frente com velocidade  (Fig.2), isto é o movimento horizontal é uniforme. Porém, o movimento de queda é uniformemente variado, a velocidade vertical vai aumentando com aceleração . 

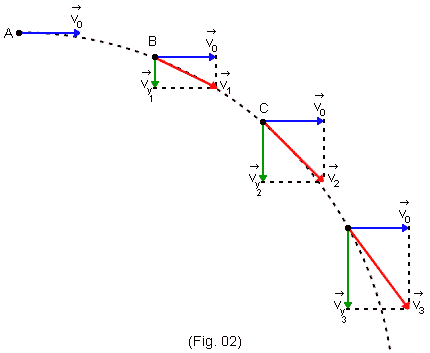
Sendo A a posição em que a bola abandona a mesa, nesse instante a velocidade da bola é  .

Algum tempo depois, quando a bola passa pela posição B, a velocidade horizontal continua sendo  . Porém, a bola já tem uma velocidade vertical , de modo que sua velocidade (total) é  , o vetor  é tangente à trajetória.

Ao passar pela posição C, a velocidade horizontal continua sendo  mas a velocidade vertical é um pouco maior ainda, sendo  a velocidade total.

Exemplo

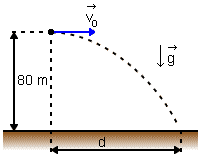
Numa região onde g = 10 m/s² uma partícula é lançada horizontalmente, de um ponto situado a 80 m de altura, com velocidade v₀ = 30 m/s como ilustra a figura

a) depois de quanto tempo a partícula chega ao solo?

b) com que velocidade a partícula atinge o solo?

c) calcule a distância d assinalada na figura.

Resolução

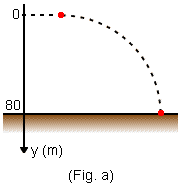
a) Os movimentos horizontal e vertical podem ser analisados separadamente. Na vertical a partícula tem um movimento uniformemente variado, de velocidade inicial nula (v_o = O). Adotando o eixo da figura, o espaço inicial também é nulo (s_o = 0)

s = s_o + v_o + t²

y = 0 + 0 +  t²

y = (5,0)t²    (I)

Quando a partícula atingir o solo teremos y = 80 m . Substituindo na equação (I) temos:

y = (5,0) . t²

80 = (5,0) . t²

t² = 16

 t = 4,0 s

b) Na vertical, a equação da velocidade é dada por:

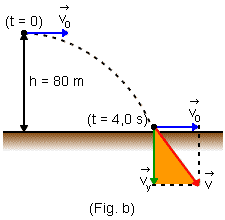
V = Vo + at

V_y = Voy + gt

V_y = 0 + 10t

V_y = 10t

No instante t = 4,0 s, temos:

V_y = 10t = 10 (4,0)

V_y = 40 m/s

Aplicando o teorema de Pitágoras ao triângulo sombreado na (Fig.b), temos:

V² = V_y² + V_o²

V² = (40)² + (30)² = 1600 + 900 = 2500

V =  = 50

 V = 50m/s

Essa velocidade poderia ser calculada usando a conservação da Energia Mecânica:

 + mgh = 

ou:

V_o² + 2gh = V²

(30)² + 2(10) (80) = V²

900 + 1600 = V²

V² = 2500

V = 50m/s

c) Na horizontal o movimento é uniforme e, assim a equação horária do espaço é do tipo:

S = S_o + vt

Com o eixo adotado na figura temos s_o = 0. Além disso, na horizontal a velocidade é V_o. Assim:

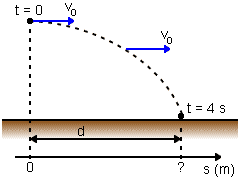
S = 0 + V_o t

S = 0 + 30 t

S = 30 t

A partícula atinge o solo no instante t = 4,0 s. Substituindo na equação anterior:

S = 30 (t)

S = 30 (4,0)

S = 120 m

Portanto:

d = 120m