Isomeria
- Home
- Isomeria
Tipos de Isomeria: Plana e Espacial
Isomeria ocorre quando vários compostos orgânicos apresentam a mesma fórmula molecular.
Para entendermos o que vem a ser isomeria, imagine para a fórmula C5H10, quais fórmulas estruturais diferentes, com seus respectivos nomes, conseguiríamos escrever?
Começaremos com alcenos (CnH2n) de cadeia normal e depois ramificada.
CH2= CH CH2 CH2 CH2 CH2 CH3 CH3 1-penteno (C5H10) |
CH3 CH= CH CH= CH CH2 CH2 CH3 CH3 2-penteno (C5H10) |
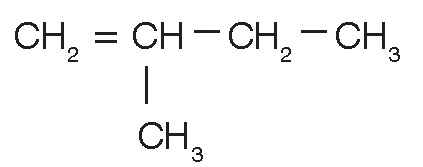 2-metil-1-buteno (C5H10) |
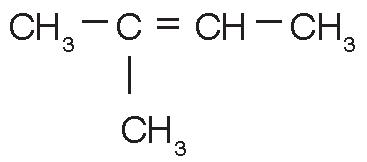 2-metil-2-buteno (C5H10) |
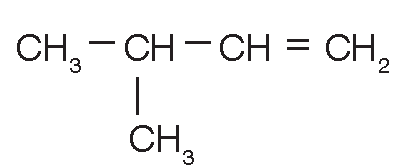 3-metil-1-buteno (C5H10) |
Agora montaremos estruturas cíclicas (ciclanos), tanto de cadeia normal e ramificada.
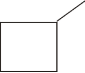
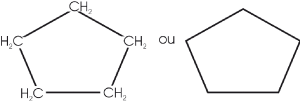 ciclo - pentano (C5H10) |
metil-ciclo-butano (C5H10) |
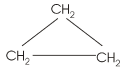
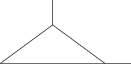 1,2-dimetil-ciclo-propano (C5H10) |
|
1,1-dimetil-ciclo-propano |
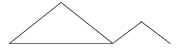 etil-ciclo-propano |
Observamos que uma fórmula molecular (C5H10) pode dar origem a várias fórmulas estruturais diferentes (10), cada uma identificando uma substância distinta quanto às suas propriedades (ponto de fusão, ponto de ebulição, estado físico, densidade). Podemos concluir então que:
| ISOMERIA É QUANDO UMA FÓRMULA MOLECULAR DÁ ORIGEM A VÁRIOS COMPOSTOS DE FÓRMULA ESTRUTURAL DIFERENTES (ISÔMEROS). |
ISOMERIA PLANA
a) Posição:
É o caso em que a mudança de posição de uma insaturação ou radical fora da cadeia principal diferencia os isômeros.
Exemplos
CH2=CH CH2
CH2 CH3 e CH3
CH3 e CH3 CH = CH
CH = CH CH3
CH3
1-buteno 2-buteno
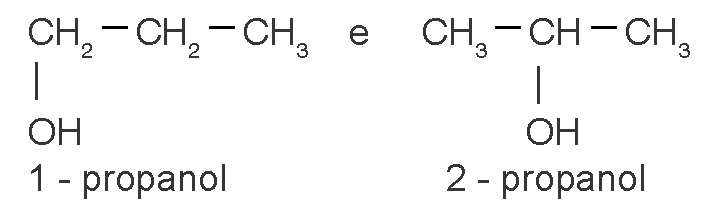
 e
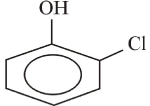
e 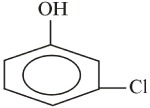
orto - cloro - fenol meta - cloro - fenol
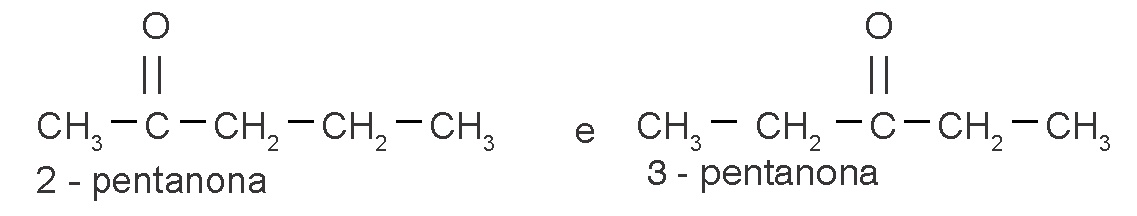
b) Cadeia:
Como o próprio nome diz, a diferença básica entre os isômeros está no tipo de cadeia (aberta ou cíclica, normal ou ramificada e homogênea ou heterogênea).
Exemplos
|
CH2=CH |
|
|
|
|
CH3  NH NH CH2 CH2 CH2 CH2 CH3 H2N CH3 H2N CH2 CH2 CH2 CH2 CH2 CH2 CH3 CH3metil-propil-amina e butil-amina (C4H11N) (heterogênea e homogênea) |
|
CH3 CH=CH CH=CH CH2 CH2 CH3 CH3 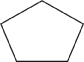 2 - penteno e ciclo pentano (C5H10) (aberta e fechada) |
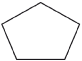 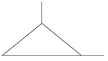 ciclo pentano e 1,2 - dimetil-ciclo-propano (C8H18) (normal e ramificada) |
c) Função:
É o tipo de isomeria plana mais importante para o vestibular!
Compostos de funções diferentes é que dão origem aos isômeros. Notamos nesse caso a maior diferença quanto às propriedades físicas e químicas para os isômeros. Estas são as situações mais comuns.
álcool / éter
CH3 CH2 CH2 OH CH3 OH CH3 O O CH3 CH3etanol e metóxi-metano (C2H6O) |
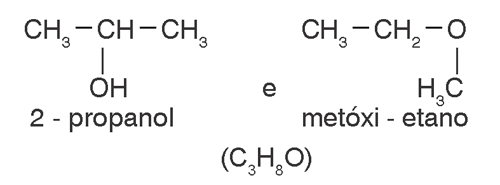 |
cetona / aldeído
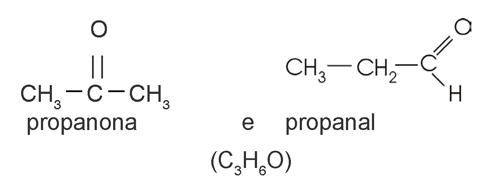 |
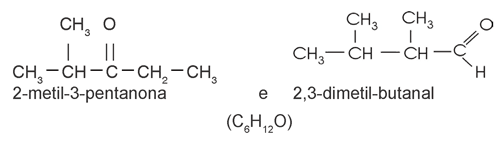 |
||
ácido carboxílico / éster
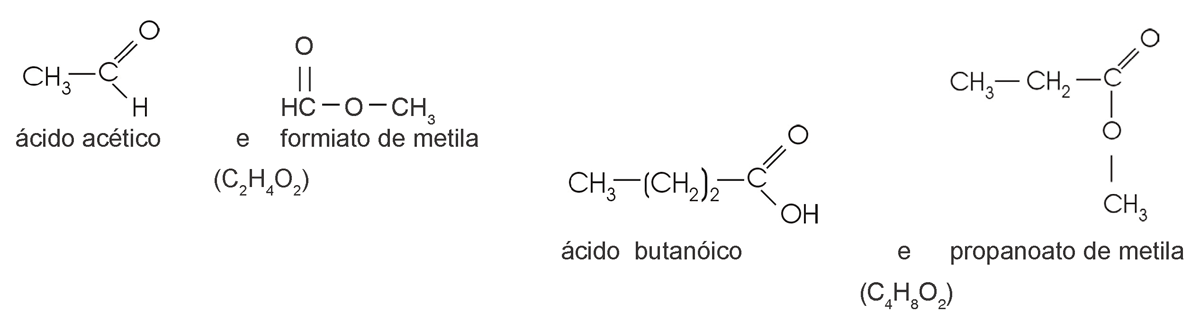
Se analisarmos, concluiremos que é possível também haver esse tipo de isomeria entre um fenol e um álcool aromático.
d) Metameria ou compensação:
Esta classe de isomeria só é possível em cadeia heterogênea, pela mudança de posição do heteroátomo, normalmente oxigênio ou nitrogênio.
Exemplos
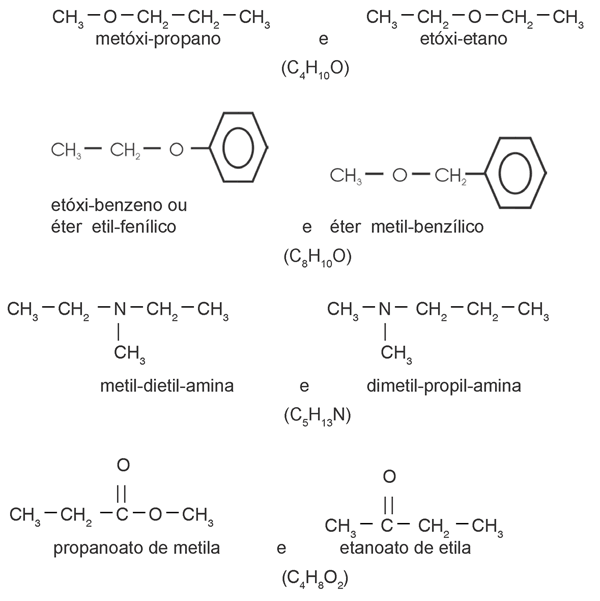
Lembre-se que os isômeros de compensação só podem existir dentro de uma mesma função, sempre de cadeia heterogênea. A função não pode mudar; caso contrário, há isomeria de função.
e) Tautomeria:
Caso particular de isomeria de função, consequência da atração entre polos elétricos contrários, formados a partir da diferença de eletronegatividade presente na ligação covalente polar. Possível entre os pares enol/aldeído; e como o aldeído é isômero funcional da cetona, também ocorre o par enol/cetona como tautômeros.
Exemplos
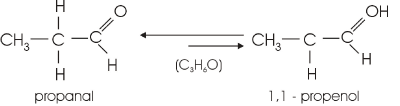
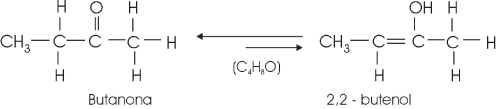
Nota-se no segundo exemplo que é o carbono da esquerda em relação à carbonila (radical da função cetona) que perde o H+ para o átomo de oxigênio, devido ao fato desse carbono possuir menor polaridade negativa (-), o que atrai menos o polo H+.
Sempre quando há um frasco com um aldeído ou com uma cetona junto com essas substâncias, haverá um enol em equilíbrio químico, onde o enol existe em menor quantidade pelo fato de ser menos estável.
ISOMERIA ESPACIAL
Neste tipo de isomeria, a diferença básica entre os isômeros está na forma ou posição de sua molécula no espaço, e não mais no plano, onde era usada simplesmente a fórmula estrutural.
Na isomeria espacial, há uma divisão, nos seguintes dois casos:
a) Cis-Trans ou Geométrica
Em cadeia aberta ou alifática, a condição necessária para este tipo de isomeria é a presença de uma dupla ligação entre dois carbonos. Cada um dos dois carbonos apresenta dois ligantes diferentes.
Para identificar os isômeros geométricos, é necessário explorar o ângulo de 120º existente na dupla ligação entre carbonos (forma espacial plana triangular). Se acima ou abaixo da dupla ligação, os ligantes forem iguais, há o isômero cis. A condição do isômero trans é a inversa do cis, ou seja, acima e abaixo da dupla, os ligantes serão diferentes.
Exemplo 1
2 - buteno
fórmula plana: CH3 CH=CH
CH=CH CH3
CH3
fórmulas espaciais:
|
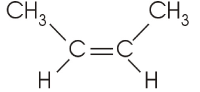
cis - 2 - buteno |
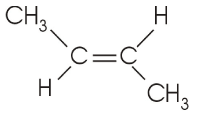 trans - 2 - buteno acima e abaixo da dupla os ligantes são diferentes |
Exemplo 2
2, 3 - dicloro - 2 - penteno
fórmula plana:
CH3 C = C
C = C CH2
CH2 CH3
CH3
| |
Cl Cl
fórmulas espaciais:
|
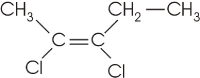
cis - 2, 3 - dicloro - 2 - penteno |
nota-se que acima e abaixo da dupla ligação, |
Um exemplo "clássico" de isomeria geométrica é o ácido butenodioico, existente na forma cis (ácido maleico) e trans (ácido fumárico), importantes em fenômenos bioquímicos.
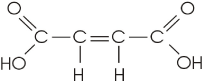 fórmula plana |
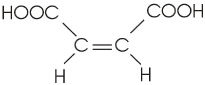 ácido cis butenodioico (ácido maleico) |
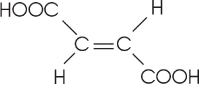 ácido trans butenodioico (ácido fumárico) |
Consequência de suas fórmulas espaciais diferentes, há propriedades físicas (ponto de fusão e ebulição, densidade, solubilidade em água) e químicas (facilidade em desidratação por aquecimento), diferentes.
|
Ácido maleico
|
Ácido fumárico
|
|
| Ponto de fusão (°C) |
130
|
287
|
| densidade (g/ml) |
1,590
|
1,635
|
| solubilidade em água |
solúvel
|
pouco solúvel
|
| Constante de ionização (Ki) |
1,170
|
0,097
|
Em cadeia fechada ou cíclica, pode haver isomeria cis-trans: basta haver dois carbonos do ciclo, vizinhos ou não, apresentando, cada um deles, dois ligantes diferentes. Nota-se que agora não é necessário a presença da dupla ligação. A forma espacial em vigor para o carbono fazendo apenas simples ligação será do tipo tetraédrica.
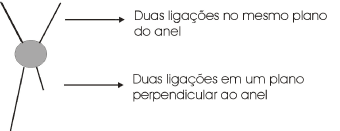
Se à frente ou atrás do plano formado pela cadeia cíclica, os ligantes forem iguais, haverá o isômero cis e se à frente e atrás deste plano os ligantes forem diferentes, haverá o isômero trans.
Exemplo
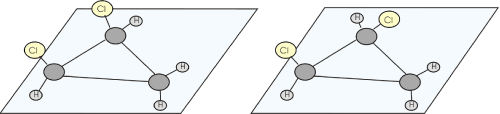
| cis-1,2-dicloro-ciclo propano 2 átomos de Cl acima do plano do anel |
trans-1,2-dicloro-ciclo propano 1 átomo de Cl acima e um abaixo do plano do anel |
b) Óptica
Antes de estudarmos esse tipo de isomeria espacial, devemos revisar alguns conceitos básicos relacionados ao fenômeno de propagação de uma onda eletromagnética (luz) no espaço.
ONDAS
Na física, entendemos como ondas toda propagação de energia em um meio, material ou não.
As ondas de acordo com a natureza (características físicas) estão divididas em mecânicas (necessitam de um meio para se propagarem) e eletromagnéticas (se propagam no vácuo).
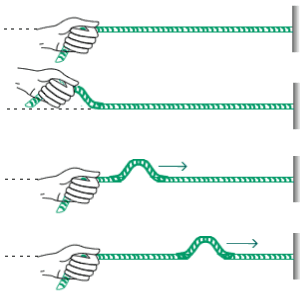
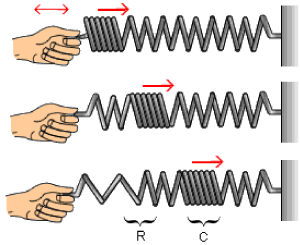
Plano de Propagação de Onda (ppo): Consideremos uma corda fixada em uma parede, segundo a ilustração a seguir. Se a essa corda uma pessoa transmitir um movimento vertical, com o passar do tempo, a energia fornecida (cinética + potencial) irá se propagar em apenas um plano de propagação, indicado a seguir:
p.p.o. vertical (senoide)
 (1)
(1)
Em uma outra situação, a pessoa transmite à corda um movimento horizontal, onde a energia mecânica fornecida se propagará também em apenas um p.p.o.
p.p.o. horizontal (senoide)
 (2)
(2)
Agora, simultaneamente, a pessoa transmitirá à corda os dois movimentos: horizontal (1) e vertical (2). Qual será o tipo de movimento resultante na corda?
É um pouco difícil de imaginar, mas o movimento final será do tipo de uma espiral, conforme a ilustração a seguir:
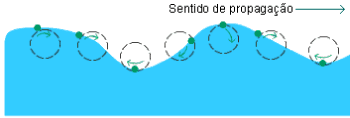
Ondas Eletromagnéticas
No estudo da eletricidade, aprendemos que as cargas elétricas em movimento produzem campo elétrico e campo magnético. Quando uma carga elétrica oscila, ela produz campos elétricos e campos magnéticos que "viajam" de modo semelhante a uma onda mecânica. Esses campos viajantes formam uma onda eletromagnética.
A luz comum é uma onda eletromagnética, ou seja, uma associação de um campo elétrico (E) e um campo magnético (B) se propagando (sempre um plano é perpendicular ao outro) em todas as direções. É por este motivo que a luz comum normalmente se "espalha" com facilidade à altíssima velocidade (no vácuo, 300.000 km/s), o que os físicos chamam de difusão.
A energia e visibilidade de uma onda eletromagnética dependerá do seu comprimento de onda (λ). Sua energia aumenta conforme diminui λ.
Luz Polarizada
Onda eletromagnética que possui apenas um p.p.o., ou seja, não sofre mais o fenômeno da difusão, se propagando sempre em uma única direção. Como exemplo, pode-se citar a luz emitida por alguns holofotes de iluminação, o raio laser e a luz emitida pelo projetor de filmes no cinema. Alguns tipos de máquinas fotográficas também usam luz polarizada (Polaroide) para sensibilizar o filme, dando mais nitidez à imagem.
A polarização da luz pode ser alcançada com conjuntos de lentes apropriadas ou por um conjunto óptico bem simples chamado de prisma de Nicol, que consiste em dois prismas sobrepostos com uma substância gelatinosa.
Carbono Assimétrico ou Quiral
A existência da isomeria óptica em compostos orgânicos está associada à presença do chamado carbono assimétrico ou quiral (*C), ou seja, um átomo de carbono que se liga a quatro ligantes diferentes.
Observa-se, na prática, que soluções aquosas que possuem carbono assimétrico em seu soluto (material dissolvido) causam desvio no p.p.o. de uma luz polarizada. Se este desvio causado for para a direita (+α) haverá dissolvido em água o isômero espacial chamado de dextrogiro ( + ). Caso contrário, se o desvio causado no p.p.o. for para a esquerda ( -α), haverá o isômero espacial levogiro ( - ). Tanto o levógiro quanto o dextrogiro são considerados opticamente ativos porque causam desvio no p.p.o. da luz polarizada.
Exemplo
ácido-2-hidróxi-propanóico ou ácido lático
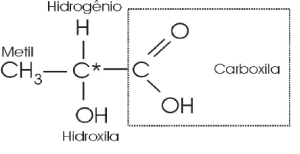
O carbono central é assimétrico.
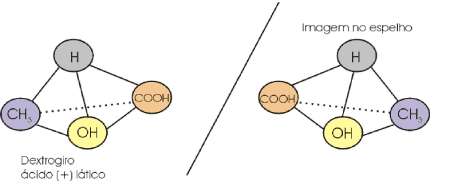
De uma forma mais simples, com o auxílio de um espelho plano, pode-se também representar os isômeros espaciais ópticos. Estes são chamados de espécies enantiomorfas ou antípodas ópticos.
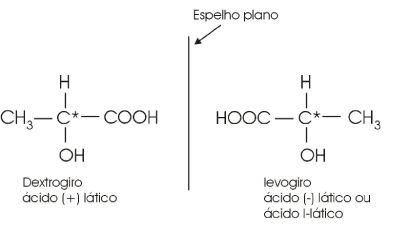
O ácido lático dextrogiro e o ácido lático levogiro têm as mesmas propriedades físicas (densidade, ponto de fusão, etc.), exceto o desvio do plano da luz polarizada.
Mistura Racêmica: Se em uma solução houver 50% de levogiro e 50% de dextrogiro dissolvidos, haverá uma mistura chamada de racêmica, que é opticamente inativa, pois não causa desvio no p.p.o. da luz polarizada.
Carbonos Assimétricos e Isômeros Ópticos
O número de isômeros ópticos para um composto orgânico vai depender do número de carbonos assimétricos presentes na sua estrutura. Havendo n carbonos assimétricos diferentes, haverá 2n isômeros ópticos diferentes.
nº de isômeros ópticos ativos = 2n
onde:
n = número de carbonos assimétricos diferentes
nº de misturas racêmicas = 2 : 2 = 2n - 1
Áreas exclusivas para assinantes