Gravitação Universal

Gravitação Universal

Os Movimentos dos Planetas

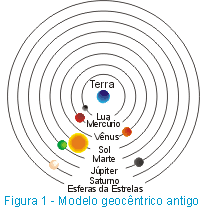
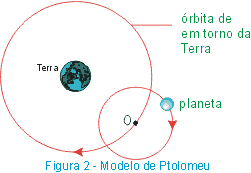
Na Grécia antiga, os primeiros filósofos propuseram modelos para explicar os movimentos dos corpos celestes. O primeiro modelo que teve, na época, uma grande aceitação foi o modelo geocêntrico (Fig. 1) assim chamado pois admitia que a Terra estaria no centro do Universo enquanto o Sol, a Lua e os planetas (até então conhecidos) girariam em órbitas circulares ao redor da Terra. Porém, esse modelo não explicava completamente as observações. Assim, Ptolomeu (100 DC - 165 DC) introduziu uma mudança nesse modelo (Fig. 2). Nesse novo modelo a Terra continuava no centro do Universo enquanto cada planeta girava em torno de um ponto o qual por sua vez tinha uma trajetória circular em torno da Terra.

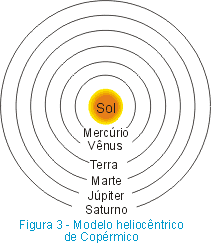
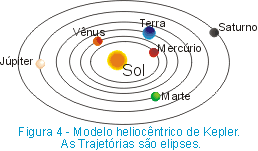
O modelo de Ptolomeu prevaleceu até o Renascimento quando o polonês Nicolau Copérnico (1473 - 1543) propôs um modelo heliocêntrico (Sol no centro) segundo o qual (Fig. 3) o Sol estaria no centro do Universo, enquanto os planetas girariam, em órbitas circulares, em torno do Sol. Porém, esse modelo também não explicava as observações. Assim, usando os dados coletados pelo dinamarquês Tycho Brahe (1546 - 1601), o astrônomo alemão Johannes Kepler (1571 - 1630) concluiu que as trajetórias dos planetas não eram circunferências mas sim elipses (Fig. 4 ).

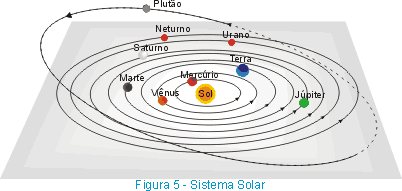
Na época de Kepler só eram conhecidos 6 planetas. Mais tarde foram descobertos Urano, Netuno e Plutão e, de acordo com os conhecimentos atuais o Sistema Solar é o representado na figura 5. As órbitas de quase todos os planetas estão aproximadamente contidas num mesmo plano. A exceção é Plutão cuja órbita está contida num plano inclinado de 17º em relação ao plano da órbita da Terra.

Obs.: Até o ano de 2006, Plutão era considerado um planeta principal do sistema solar. Porém, foram descobertos vários corpos celestes de tamanha comparável ao de Plutão. Por este motivo, Plutão passou a ser considerado um "planeta anão", também sendo denominado de "plutoide".

Leis de Kepler

Analisando cuidadosamente os dados coletados por Tycho Brahe, Kepler chegou a três leis sobre os movimentos dos planetas.

Primeira lei de Kepler

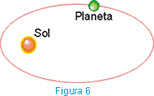
Cada planeta gira em torno do Sol de modo que sua trajetória é uma elipse, estando o Sol num dos focos da elipse.

Segunda lei de Kepler

O segmento que liga o Sol a um planeta varre áreas proporcionais aos tempos gastos para o percurso.

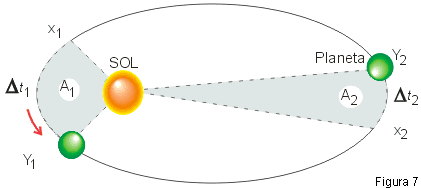
Assim, por exemplo, no caso da Fig. 7, se o planeta gasta um tempo Δt₁ para percorrer o trecho X₁Y₁ e um tempo Δt₂ para percorrer o trecho X₂Y₂, temos:

Observando a Fig. 7 percebemos que uma consequência dessa lei é que a velocidade do planeta não é constante durante o seu percurso. Quanto mais perto do Sol, maior a velocidade do planeta e, à medida que se afasta do Sol, sua velocidade diminui.

Terceira Lei de Kepler

Sendo T o período do movimento do planeta em torno do Sol e R o comprimento do semieixo maior da trajetória, temos:

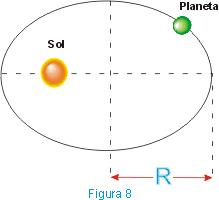
O comprimento do semieixo maior (R) é também chamado de distância média ao Sol.

Se a trajetória for circular, o valor de R é o raio da circunferência.

Mais tarde, pela aplicação da Lei de Newton ( que veremos adiante ), demonstrou-se que as leis de Kepler valem para qualquer sistema onde existem corpos girando em torno de um corpo de massa muito maior, como por exemplo no caso da Lua e dos satélites artificiais girando em torno da Terra.

Exemplo 1

A distância média da Terra ao Sol é dada por . Sabendo que a distância média de Marte ao Sol é , calcule o tempo que Marte demora para dar uma volta em torno do Sol.

Resolução

Queremos determinar o período (T_M) do movimento de Marte; o período do movimento da Terra é conhecido:

Pela terceira lei de Kepler temos:

T_M = 1,9 anos terrestres

Lei da Gravitação Universal

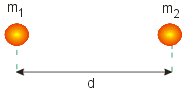
Em 1687, em sua famosa obra "Princípios Matemáticos da Filosofia Natural" , Isaac Newton (1642 - 1727) mostrou que as leis de Kepler podiam ser demonstradas admitindo que entre um par qualquer de partículas, de massas m₁ e m₂ (Fig. 9 ), existe um par de forças de atração cujas intensidades são dadas por:

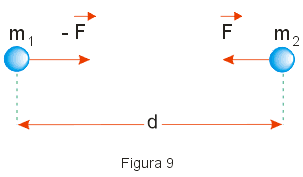
onde d é a distância entre as partículas e G é uma constante, denominada constante de gravitação universal e cujo valor no Sistema Internacional de Unidades é:

Para calcular a força de atração entre corpos de tamanhos não desprezíveis devemos dividi-los em pequenos corpúsculos, calcular a força de atração entre cada par e depois efetuar a soma. Esse processo em geral é complexo, exigindo a aplicação do Cálculo Integral. No entanto há um caso particular demonstrado por Newton:

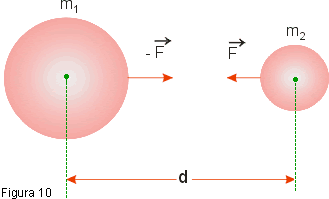
Exemplo 1

Duas pessoas, de massas M = 80 kg e m = 60 kg estão de pé, separados por uma distância 

d = 3,0 metros. Calcule o valor aproximado das intensidades das forças de atração gravitacional que há entre eles.

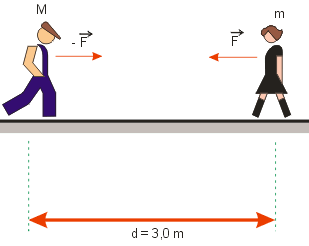
Resolução

Pela lei da gravitação de Newton temos:

F 3,5 . 10^-8N

Como podemos observar, essa força tem intensidade muito pequena de modo que não a percebemos. Para que a força gravitacional tenha intensidade perceptível, pelo menos uma das massas deve ser "muito grande", como é caso dos planetas.

Corpos em Órbita Circular

Consideremos um corpo de massa m  girando em torno de um corpo de massa M de modo que M seja  "muito maior" do que m ( M » m ). Desse modo podemos supor o corpo de maior massa como estando praticamente em repouso e considerar apenas o movimento do corpo de massa menor. Supondo que a trajetória seja circular de raio R (Fig. 11), a força de atração gravitacional  fará o papel de uma força centrípeta:

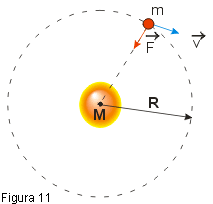Como podemos observar, a velocidade do corpo de massa m não depende do valor dessa massa, mas apenas da massa do corpo central (M).

Exemplo 2

Um satélite artificial gira em torno da Terra, em órbita circular situada a uma altura h = 1600 km acima da superfície da Terra. São dados:

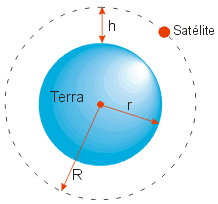
Calcule o tempo que o satélite gasta para dar uma volta completa em torno da Terra.

Resolução

A órbita do satélite tem raio R dado por:

R = r + h = ( 6400 km ) + ( 1600 km ) = 8 000 km = 8,0.10⁶ m

Na teoria vimos que:

O período do movimento do satélite é:

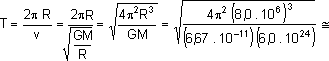
Campo Gravitacional

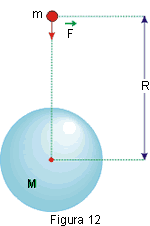Consideremos um "pequeno" corpo de massa m situado a uma distância R do centro da Terra, como mostra a Fig. 12.

A Terra exercerá sobre o corpo uma força de atração gravitacional cuja intensidade é:

onde M é a massa da Terra. Supondo que essa seja a única força atuante no corpo, pela Segunda lei de Newton teremos:

onde é a aceleração do corpo. Assim:

Essa aceleração é a aceleração da gravidade ( g ), também chamada de campo gravitacional.

Assim, temos:

Portanto vemos que a aceleração da gravidade diminui à medida que nos afastamos da Terra. Porém quando consideramos uma região de pequena altura próximo à superfície da Terra, o valor de g pode ser considerado aproximadamente constante dentro dessa região, sendo dado por g ≅ 9,8m/s².

O cálculo que fizemos supõe a Terra como sendo esférica e homogênea o que não é verdade e assim, na realidade, o valor de g próximo à superfície da Terra depende do ponto considerado.

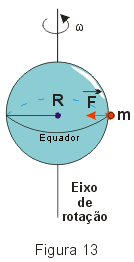
A rotação da Terra afeta o valor medido de g, também chamado de aceleração aparente da gravidade (g_a). Para percebermos isso consideremos, por exemplo, um corpo de massa m situado no equador (Fig. 13).

Esse corpo recebe da Terra uma força de atração gravitacional dada por:

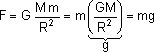
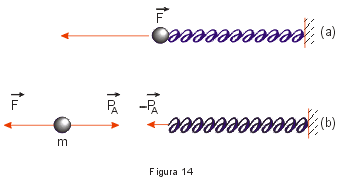
Se colocarmos esse corpo na extremidade de um dinamômetro (Fig. 14) ele receberá do dinamômetro uma força cuja intensidade é o peso aparente, sendo dado por:

P_A = m . g_A

Como o corpo está em movimento circular e uniforme, de velocidade angular , a resultante de é a força centrípeta :

Assim:

Supondo a Terra esférica e homogênea, nos polos a gravidade medida é o próprio g.

Energia Potencial

Pode-se demonstrar que a força gravitacional é conservativa e, portanto, podemos definir uma energia potencial. Adotando referencial no infinito, isto é, considerando a energia potencial de um par de partículas como sendo nula quando estiverem infinitamente afastadas, a energia potencial é dada por:

Velocidade de Escape

Chamamos de velocidade de escape de um planeta, a menor velocidade v_E que devemos dar a um corpo para que ele nunca mais volte ao planeta.

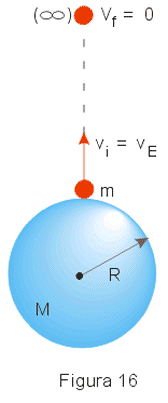
Suponhamos então um corpo de massa m lançando com velocidade inicial v_i  =  v_E  a partir da superfície de um planeta de raio R (Fig. 16 ).

Suponhamos que ele só atinja velocidade nula no infinito.

Temos então:

Pelo princípio da conservação da energia mecânica temos:

Portanto:

Exemplo 3

Sabendo que a massa e o raio da Terra são, respectivamente, M = 6,0.10 ²⁴ kg e R = 6, 4.10⁶m, calcule a velocidade de escape da Terra.

Resolução

Sabendo que G = 6,67.10^-4 Nm²/kg², temos, temos: