Grandezas Vetoriais
- Home
- Grandezas Vetoriais
Grandezas Vetoriais
Grandezas Escalares e Vetoriais
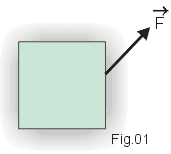
Há algumas grandezas que para ficarem caracterizadas necessitam apenas de um número (e, naturalmente, a unidade usada). É o caso, por exemplo, da temperatura, da massa, etc. Essas grandezas são chamadas escalares. Porém há outras grandezas que necessitam de uma informação adicional que nos dá a direção e o sentido da grandeza. É o caso, por exemplo, da força. Quando aplicamos uma força a um corpo (Fig.1), além do valor da força, desenhamos um segmento orientado para dizer "para que lado" atua a força. As grandezas que necessitam dessa informação geométrica são denominadas grandezas vetoriais e os segmentos orientados usados para representá-las são denominados vetores. Para representar um vetor usamos uma letra com uma pequena flecha em cima, como indicado na Fig.1.
Nos casos mais elementares analisados até agora, a velocidade e a aceleração foram tratadas como grandezas escalares. No entanto elas são grandezas vetoriais e assim devem ser consideradas, em casos mais complexos, como veremos mais tarde.
Quando dois vetores são paralelos dizemos que eles têm a mesma direção. Se, além disso, eles apontarem para o "mesmo lado", dizemos que têm o mesmo sentido; se apontarem para "lados opostos" dizemos que têm sentidos opostos.
Suponhamos, por exemplo, o caso da Fig.2 onde as retas r, s e t são paralelas.
Podemos dizer que:
- os vetores
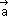 e
e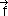 têm direções diferentes;
têm direções diferentes; - os vetores
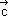 e
e 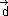 têm a mesma direção e o mesmo sentido;
têm a mesma direção e o mesmo sentido; - os vetores
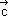 e
e 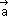 têm a mesma direção mas sentidos opostos.
têm a mesma direção mas sentidos opostos. - os vetores
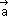 e
e 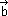 têm a mesma direção e o mesmo sentido; e
têm a mesma direção e o mesmo sentido; e - os vetores
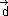 e
e 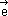 têm a mesma direção mas sentidos opostos.
têm a mesma direção mas sentidos opostos.
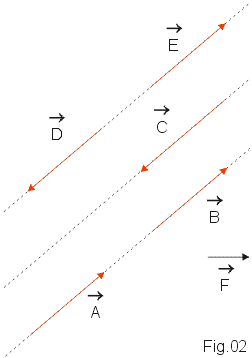
O "tamanho" do vetor é proporcional ao valor da grandeza que está representando e esse valor, considerado positivo (ou nulo), é chamado módulo do vetor. Para representar o módulo de um vetor ![]() usamos a notação |
usamos a notação | ![]() | .
| .
Quando uma grandeza tem o valor nulo, o vetor que a representa é o vetor nulo; representado por ![]() e cujo módulo é nulo.
e cujo módulo é nulo.
Dizemos que dois vetores são iguais quando, e somente quando, têm a mesma direção, o mesmo sentido e o mesmo módulo.
Adição de Vetores
Na Fig. 3 representamos dois vetores não nulos ![]() e
e ![]() . Para obtermos a soma (
. Para obtermos a soma ( ![]() ) dos vetores podemos efetuar uma translação em um dos vetores ( Fig. 4 ) de modo que a extremidade do primeiro coincida com a origem do segundo. O vetor soma é obtido ligando-se a origem do primeiro à extremidade do segundo.
) dos vetores podemos efetuar uma translação em um dos vetores ( Fig. 4 ) de modo que a extremidade do primeiro coincida com a origem do segundo. O vetor soma é obtido ligando-se a origem do primeiro à extremidade do segundo.
Para obtermos o módulo de ![]() usamos a lei dos cossenos:
usamos a lei dos cossenos:
| s |2 = | ![]() |2 + |
|2 + | ![]() |2 - 2 |
|2 - 2 | ![]() | . |
| . | ![]() | . cos θ
| . cos θ
Quando os vetores têm a mesma direção, temos uma situação mais simples, como ilustra a Fig. 5.
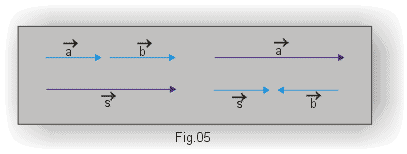
Se tivermos mais de dois vetores podemos usar o mesmo procedimento, como ilustra a Fig. 6.
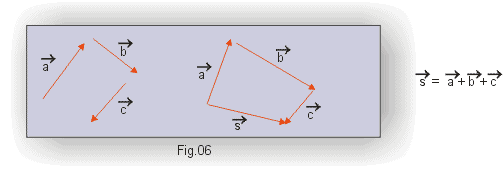
O modo de obter a soma de vetores que acabamos de descrever é conhecido como regra do polígono. Há, porém, um outro modo, que veremos adiante, conhecido como regra do paralelogramo.
Regra do Paralelogramo
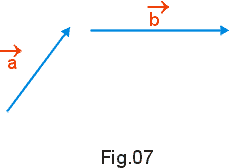
Na Fig.7 representamos dois vetores ![]() e
e ![]() .Para obtermos sua soma pela regra do paralelogramo transladamos um dos vetores de modo que tenham a mesma origem (Fig. 8). A seguir desenhamos o segmento
.Para obtermos sua soma pela regra do paralelogramo transladamos um dos vetores de modo que tenham a mesma origem (Fig. 8). A seguir desenhamos o segmento ![]() paralelo ao vetor
paralelo ao vetor ![]() e o segmento
e o segmento ![]() paralelo ao vetor
paralelo ao vetor ![]() , obtendo o paralelogramo XYZK. O segmento orientado
, obtendo o paralelogramo XYZK. O segmento orientado ![]() ( diagonal do paralelogramo) representa a soma
( diagonal do paralelogramo) representa a soma ![]() dos vetores.
dos vetores.
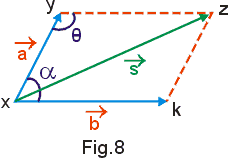
Aplicando a lei dos cossenos ao triângulo XYZ temos:
| ![]() | 2 = |
| 2 = | ![]() |2 + |
|2 + | ![]() |2 - 2 |
|2 - 2 | ![]() | . |
| . | ![]() | . cos θ
| . cos θ
Como ![]() e
e![]() são suplementares, temos cos θ= -cos α. Assim , a equação acima pode ser escrita:
são suplementares, temos cos θ= -cos α. Assim , a equação acima pode ser escrita:
| ![]() |2 = |
|2 = | ![]() |2 + |
|2 + | ![]() |2 + 2 |
|2 + 2 | ![]() | . |
| . | ![]() | . cos α
| . cos α
Exemplo 1
Para os vetores representados na figura abaixo temos:
| ![]()
![]() | = 6
| = 6
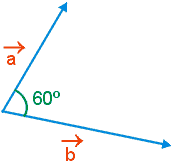
Determine o módulo da soma desses vetores.
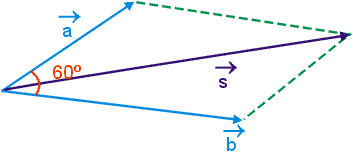
Resolução
|![]() |2 = |
|2 = | ![]() |2+ |
|2+ | ![]() |2 + 2 |
|2 + 2 | ![]() | . |
| . | ![]() | . cos 60º
| . cos 60º
Lembrando que cos 60º = ![]()
| ![]() |2 = 42 + 62 + 2 ( 4 ) ( 6 ) (
|2 = 42 + 62 + 2 ( 4 ) ( 6 ) ( ![]() )
)
| ![]() |2 = 16 + 36 + 24
|2 = 16 + 36 + 24
| ![]() |2 = 76
|2 = 76
| ![]() | =
| = ![]() =
= ![]() = 2
= 2 ![]()
![]() 8,7
8,7
A soma de dois vetores é também chamada de resultante dos dois vetores.
Oposto de um vetor
Dado um vetor não nulo ![]() , o seu oposto é representado por -
, o seu oposto é representado por -![]() , e tem as seguintes características (Fig. 9):
, e tem as seguintes características (Fig. 9):
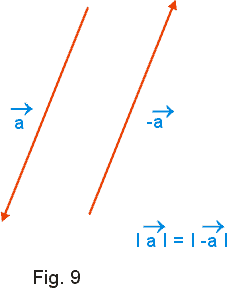
- mesma direção de
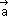
- mesmo módulo de
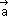
- sentido oposto ao de
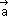
O oposto do vetor nulo é ele mesmo:
-![]() =
= ![]()
Subtração de vetores
Dados dois vetores ![]() e
e ![]() , a diferença
, a diferença ![]() entre
entre ![]() e
e ![]() é indicada por:
é indicada por:
![]() =
= ![]() -
- ![]()
e é definida do seguinte modo:
![]() =
= ![]() -
- ![]() =
= ![]() + ( -
+ ( - ![]() )
)
isto é, a diferença entre ![]() e
e ![]() é igual à soma de
é igual à soma de ![]() com o oposto de
com o oposto de ![]() .
.
Exemplo 2
Para os vetores representados abaixo, determine o vetor ![]() tal que
tal que ![]() =
= ![]() -
- ![]()
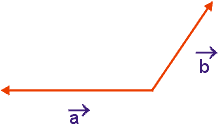
Resolução
Por definição temos:
![]() =
= ![]() + ( -
+ ( -![]() )
)
Na figura abaixo representamos o vetor -![]() e a seguir, pela regra do paralelogramo, determinamos a soma de
e a seguir, pela regra do paralelogramo, determinamos a soma de ![]() com -
com -![]() .
.
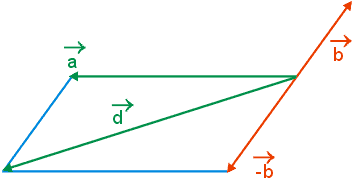
Multiplicação de um vetor por um número
Dado um vetor não nulo ![]() e um número real não nulo k, a multiplicação de kpor
e um número real não nulo k, a multiplicação de kpor ![]() resulta num vetor
resulta num vetor ![]() , indicado por
, indicado por
![]() = k .
= k . ![]()
e tal que:
-1º ) | ![]() | = | k | . |
| = | k | . | ![]() |
|
-2º ) ![]() e
e ![]() têm a mesma direção
têm a mesma direção
-3º) 
Exemplo 3
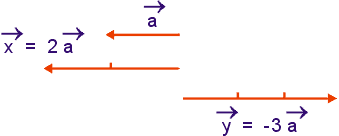
Na figura abaixo representamos o vetor ![]() , o vetor
, o vetor ![]() tal que
tal que ![]() = 2
= 2 ![]() e o vetor
e o vetor ![]() tal que
tal que ![]() = -3
= -3 ![]() .
.
Podemos observar que:
| ![]() | = 2 |
| = 2 | ![]() | e |
| e | ![]() | = 3 |
| = 3 | ![]() |
|
Se ![]() =
= ![]() ou k = 0 temos:
ou k = 0 temos:
k . ![]() =
= ![]()
Decomposição de um vetor
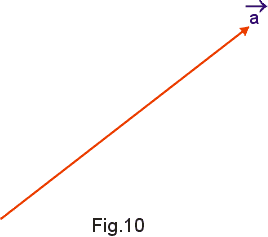
Dado um vetor ![]() não nulo (Fig.10), como veremos mais tarde, pode ser vantajoso obter dois vetores perpendiculares
não nulo (Fig.10), como veremos mais tarde, pode ser vantajoso obter dois vetores perpendiculares ![]() e
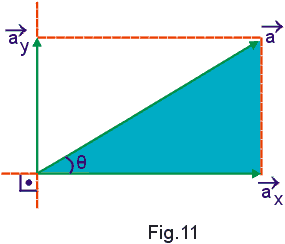
e ![]() (Fig. 11) tais que:
(Fig. 11) tais que:
![]() =
= ![]() +
+ ![]()
Esse processo é chamado decomposição, dizemos que o vetor ![]() foi decomposto nos vetores
foi decomposto nos vetores ![]() e
e ![]() . Feita a decomposição, o vetor
. Feita a decomposição, o vetor ![]() é substituído pelo par de vetores
é substituído pelo par de vetores ![]() e
e ![]() . (Fig. 12)
. (Fig. 12)
|
|
|
|
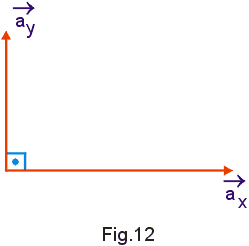
Considerando o triângulo sombreado na Fig. 11 temos:
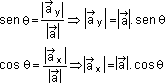
Exemplo 4
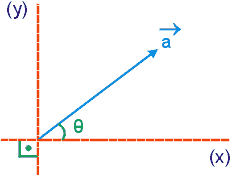
Para o vetor ![]() representado abaixo temos |
representado abaixo temos | ![]() | = 5. Sabendo que sen θ = 0,8 e cos θ = 0,6 , determine os módulos dos vetores obtidos pela decomposição do vetor
| = 5. Sabendo que sen θ = 0,8 e cos θ = 0,6 , determine os módulos dos vetores obtidos pela decomposição do vetor ![]() nas direções x e y.
nas direções x e y.
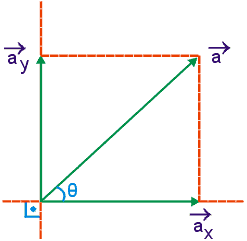
Resolução
| ![]() | = |
| = | ![]() | . cos θ = ( 5 ) ( 0,6 ) = 3
| . cos θ = ( 5 ) ( 0,6 ) = 3
| ![]() | = |
| = | ![]() | . sen θ = ( 5 ) ( 0,8 ) = 4
| . sen θ = ( 5 ) ( 0,8 ) = 4
Sumário
- Grandezas Escalares e Vetoriais
- Adição de Vetores
- Regra do Paralelogramo
- Oposto de um vetor
- Subtração de vetores
- Multiplicação de um vetor por um número
- Decomposição de um vetor
Áreas exclusivas para assinantes