Funções Exponenciais - Funções Logarítmicas
- Home
- Funções Exponenciais Funções Logarítmicas
Funções Exponenciais - Funções Logarítmicas
Função exponencial
Para cada número real b (positivo e diferente de 1) podemos construir uma função chamada função exponencial com base b, cujo domínio é o conjunto de todos os números reais e cuja fórmula (equação) é y = bx. Por exemplo
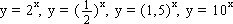
|
Função exponencial Para toda constante real b, b > 0 e b ≠ 1 a equação y = bx define uma função exponencial com base b, cujo domínio é o conjunto dos números reais. |
Observação
Usamos b > 0 para evitarmos raízes reais de números negativos; por exemplo
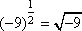
E, impomos b ≠ 1 porque y = 1x = 1 define uma função constante.
Vamos examinar o comportamento da função exponencial com base 2
y = f(x) = 2x
1. A função é definida para todos os valores reais de x; por exemplo
x = 2: f(2) = 22 = 4
x = -2: f(-2) = 2-2 = 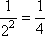
O domínio da função é o conjunto dos números reais.
2. Para todo valor de x, 2x não assume o valor zero ou valores negativos.
O conjunto imagem da função é o conjunto dos números reais positivos.
3. Com uma tabela de valores podemos esboçar o gráfico de f(x) = 22.
|
x |
f(x) |
(x; f(x)) |
|
-1 |
|
(-1; |
|
0 |
1 |
(0; 1) |
|
1 |
2 |
(1; 2) |
|
2 |
4 |
(2; 4) |
|
3 |
8 |
(3; 8) |
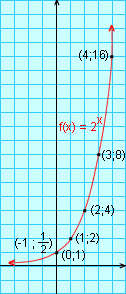
Se desejarmos, podemos melhorar a exatidão do gráfico, marcando mais pontos. Por exemplo, para valores racionais (fracionários) de x, como 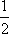 e
e 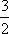 , temos
, temos
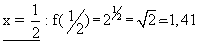
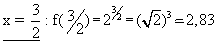
Podemos também substituir x por valores irracionais, como 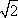 ou
ou 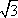 ; para efetuar os cálculos podemos usar uma calculadora científica.
; para efetuar os cálculos podemos usar uma calculadora científica.
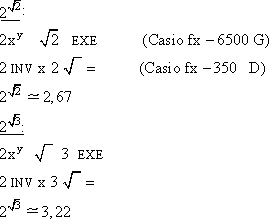
Note que os pontos 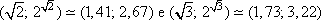 se ajustam bem à nossa curva.
se ajustam bem à nossa curva.
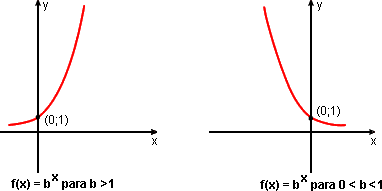
Os gráficos das funções exponenciais y = bx, com base b > 1, têm basicamente o mesmo comportamento do gráfico de y = 2x, que desenhamos.
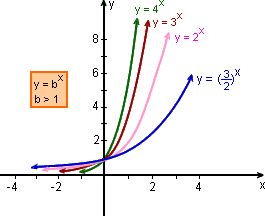
Vemos que as curvas são crescentes, com a concavidade voltada "para cima". Todas passam pelo ponto (0;1).
Vamos agora examinar os comportamentos da função exponencial com base 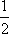
y = f(x) = 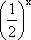
1. A função é definida para todos os valores reais de x; por exemplo
x = 2 : f(2) = 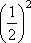 =
= 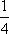
x = -2 : f(-2) = 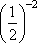 = 22 = 4
= 22 = 4
O domínio da função é o conjunto dos números reais.
2. Para todo valor de x, 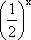 não assume o valor zero ou valores negativos.
não assume o valor zero ou valores negativos.
O conjunto imagem da função é o conjunto dos números reais positivos.
3. Com uma tabela de valores podemos esboçar o gráfico de f(x) = 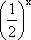 .
.
|
x |
f(x) |
(x; f(x)) |
|
-3 |
8 |
(-3; 8) |
|
-2 |
4 |
(-2; 4) |
|
-1 |
2 |
(-1; 2) |
|
0 |
1 |
(0; 1) |
|
1 |
|
(1; |
|
2 |
|
(2; |
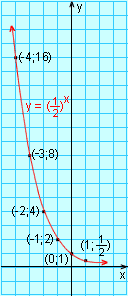
Os gráficos das funções exponenciais y = bx, com base 0 < b < 1, têm basicamente o mesmo comportamento do gráfico de y = 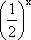 .
.
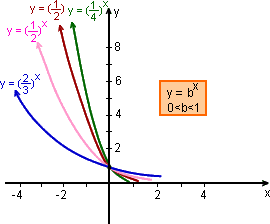
Vemos que as curvas são decrescentes, com a concavidade voltada "para cima". Todas passam pelo ponto (0; 1).
Note também que o gráfico de y = 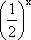 = 2-x pode ser obtido do gráfico de y = 2x por reflexão em torno do eixo-y.
= 2-x pode ser obtido do gráfico de y = 2x por reflexão em torno do eixo-y.
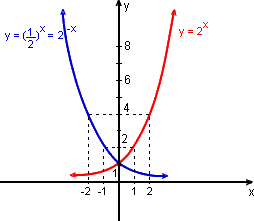
De um modo geral, isso se dá quando desenhamos o gráfico de uma equação y = f(x) e da equação y = f(-x), obtida de y = f(x) trocando x por -x.
|
Função exponencial Para b > 0 e b ≠ 1, a função exponencial com base b é definida por f(x) = bx O domínio de f é o conjunto |
Exercícios
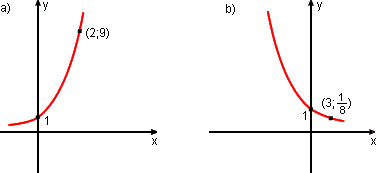
1. Determine a função exponencial f(x) = bx, cujo gráfico é dado.
Resolução
a) Se o gráfico passa por (2; 9), então f(2) = 9
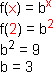
O gráfico dado é o da função exponencial com base 3.
b) Se o gráfico passa por (3;  ), então f(3) =
), então f(3) = 
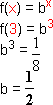
O gráfico dado é o da função exponencial com base 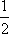 .
.
2. Usar o gráfico de y = 2x para obter o gráfico de cada uma das funções.
a) f(x) = - 2x
b) f(x) = 2x - 1
c) f(x) = 2x + 1
Resolução
a) 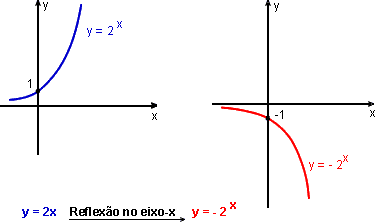
b) 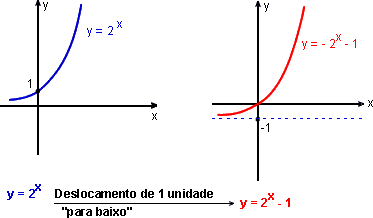
c)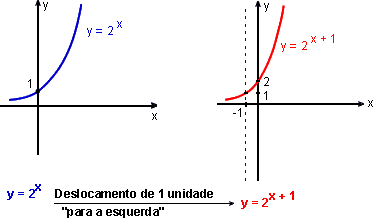
Equações exponenciais
A função exponencial com base b, b > 0 e b ≠ 1,
f(x) = bx
apresenta a seguinte propriedade:
Se f(x1) = f(x2), então x1 = x2
isto é,
Se bx1 = bx2 , então x1 = x2
Em propriedade pode ser usada para resolvermos equações exponenciais, que são equações nas quais a incógnita se apresenta nos expoentes de potências.
Por exemplo,
2x - 1 = 16
é uma equação exponencial. Para resolvê-la, observe que 16 = 24; então, escrevemos
2x - 1 = 24
e, pela propriedade descrita acima, obtemos
x - 1 = 4
x = 5.
Exercícios
1. Resolver a equação 2x2 - x = 64
Resolução
Como 64 = 26, temos:
2x2 - x = 26
x2 - x = 6
Daí,
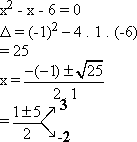
2. Resolver a equação 3x = ![]()
Resolução
Temos
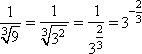
Então, a equação escreve-se assim
3x = ![]()
x = - 
3. Resolva a equação 2x + 1 + 2x = 12.
Resolução
Temos:
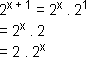
Então, a equação escreve-se assim

4. Resolva a equação ![]() = 2x . 213
= 2x . 213
Resolução
Sendo 2x . 213 = 2x + 13, vem
2x2 + 1 = 2x + 13
x2 + 1 = x + 13
Daí,
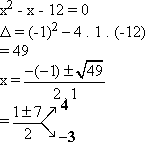
5. Seja a função exponencial com base 2, f(x) = 2x.
Se f(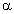 ) = m, f(
) = m, f(![]() ) = n, calcule em função de m e n:
) = n, calcule em função de m e n:
a) f (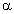 +
+ ![]() )
)
b) f (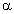 -
- ![]() )
)
c) f (5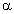 -
- ![]() )
)
Resolução
a) Temos: 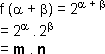
b) Temos:
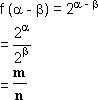
c) Temos:
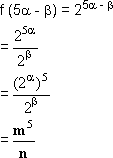
Função Logarítmica
Uma função exponencial y = f(x) = bx, com base b > 0 e b ≠ 1, é uma função 1 - 1.
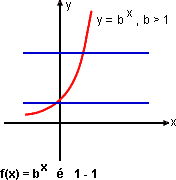
Então, ela admite uma função inversa f-1, que se chama função logarítmica com base b, que é representada com logb. Para expressarmos essa função inversa na forma y = f-1(x), isto é, para obtermos a fórmula que a define, resolvemos a equação y = bx para x, e, em seguida, trocamos x com y. Daí, a definição.
|
Função logarítmica Se b > 0 e b ≠ 1, a função logarítmica de base b é definida por y = f(x) = O domínio da função logarítmica é o conjunto dos números reais positivos. O conjunto imagem da função logarítmica é o conjunto dos números reais. |
Em outras palavras, dizemos que
|
|
Lemos 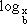 assim "logaritmo de x na base b" ou simplesmente "log de x na base b".
assim "logaritmo de x na base b" ou simplesmente "log de x na base b".
Note da definição de logaritmos, que podemos passar da forma logarítmica 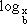 = y para a forma exponencial by = x, e que nas duas formas a base é a mesma:
= y para a forma exponencial by = x, e que nas duas formas a base é a mesma:
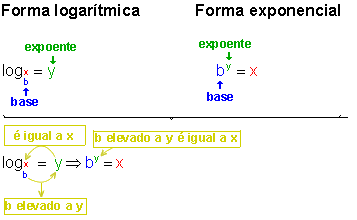
Exemplos
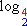 = 2 porque 22 = 4
= 2 porque 22 = 4
 = 1 porque 51 = 5
= 1 porque 51 = 5
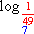 = -2 porque 7-2 =
= -2 porque 7-2 = 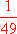
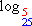 =
=  porque
porque 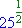 = 5
= 5
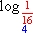 = -2 porque 4-2 =
= -2 porque 4-2 = 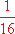
|
|
Observação
Sendo o domínio da função logarítmica limitado ao conjunto dos números reais positivos, é impossível determinamos o logaritmo de zero, o logaritmo de números negativos e de números não reais.
Exercícios
1. Calcular y em cada equação
a) ![]() = y
= y
b) ![]() = y
= y
c) ![]() = y
= y
Resolução

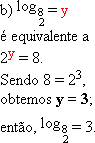
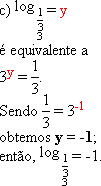
2. Em cada equação determine x.
a) ![]() =
= ![]()
b) ![]() = -1
= -1
c) ![]() = 2
= 2
Resolução
a) Temos:
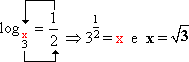
b) Temos:
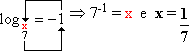
c) Temos:
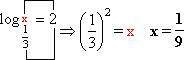
3. Em cada equação determine b.
a) ![]() = 2
= 2
b) ![]() = -1
= -1
c) ![]() =
= ![]()
Resolução
a) Temos:
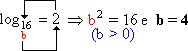
b) Temos:
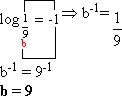
c) Temos:

Observação
Em qualquer base b, o logarítmo do número 1 é zero e o logarítmo da própria base é 1.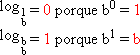
Logaritmo comum
Para fins práticos, os logaritmos com base 10 são muito usados. Os logaritmos com base 10 são chamados de logaritmos comuns ou logaritmos decimais.
Quando a base b é omitida na notação logx, fica convencionado que b = 10.
|
logx significa |
|
x |
log x |
|
|
- 2 |
|
|
- 1 |
|
log 1 |
0 |
|
log 10 |
1 |
|
log 100 |
2 |
|
log 1000 |
3 |
As calculadoras científicas nos dão o logaritmo decimal de um número positivo; por exemplo, se desejamos log 7,14, veja como operamos.
|
log 7.14 EXE (Casio fx - 6500 G) A calculadora nos mostra 0.8536982118 7.14 log (Casio fx - 350 D) A calculadora nos mostra 0.8536982 |
Logaritmo natural
Há um número, representado por e, que exerce um papel muito importante na matemática e, mais particularmente, na construção de modelos matemáticos para a descrição de fenômenos naturais.
Esse número é irracional e tem o valor aproximado
|
e = 2,718281828459... |
Os logaritmos com base e chamam-se logaritmos naturais. Os logaritmos naturais são comumente representados com ln x.
|
ln x significa |
As calculadoras científicas também dão o logaritmo natural de um número positivo. Veja, por exemplo, ln 5,92.
|
ln 5.92 EXE (Casio fx - 6500 G) A calculadora nos mostra 1.778336 449 5.92 ln (Casio fx - 350 D) A calculadora nos mostra 1.7783364 |
Gráfico da função logarítmica
Seja f uma função 1 - 1 cujo domínio é A e conjunto imagem B. Ela admite uma inversa f-1, cujo domínio é B e conjunto imagem A.
Para a função exponencial f(x) = bx, com base b > 0 e b ≠ 1, o domínio é o conjunto 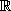 dos números reais e o conjunto imagem, o conjunto dos números reais positivos. Sua função inversa é a função logarítmica f-1(x) =
dos números reais e o conjunto imagem, o conjunto dos números reais positivos. Sua função inversa é a função logarítmica f-1(x) = 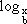 , cujo domínio é o conjunto dos números reais positivos e, conjunto imagem
, cujo domínio é o conjunto dos números reais positivos e, conjunto imagem 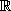 .
.
O gráfico de f-1(x) = 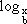 , é obtido por reflexão do gráfico de f(x) = bx com relação à reta de equação y = x.
, é obtido por reflexão do gráfico de f(x) = bx com relação à reta de equação y = x.
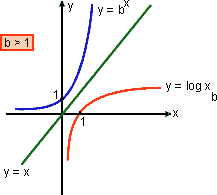
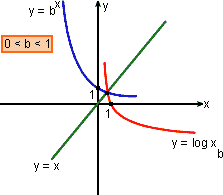
Note que quando a base b > 1, a curva é crescente, com a concavidade voltada "para cima". Ela passa pelo ponto (1; 0).
Quando 0 < b < 1, a curva é decrescente, com a concavidade também voltada "para cima"; ela passa pelo ponto (1; 0).
Exercícios
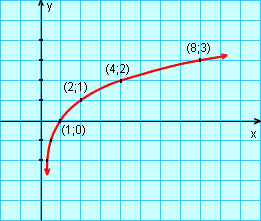
1. Esboçar o gráfico de f(x) = ![]() .
.
Resolução
Construímos uma tabela de valores para esboçar o gráfico de f(x) = ![]() ,
,

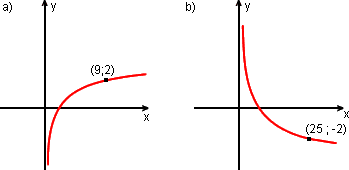
2. Determinar a função logarítmica f(x) = ![]() , cujo gráfico é dado.
, cujo gráfico é dado.
Resolução
a) Se o gráfico passa por (9; 2), então f(9) = 2.
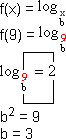
O gráfico dado é o da função logarítmica f(x) = ![]() .
.
b) Se o gráfico passa por (25; -2), então f(25) = -2.
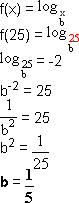
O gráfico dado é o da função logarítmica f(x) = 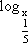 .
.
3. Usar o gráfico de y = ![]() para obter o gráfico de cada uma das funções.
para obter o gráfico de cada uma das funções.
a) f(x) = - ![]()
b) f(x) = ![]()
c) f(x) = 1 + ![]()
d) f(x) = ![]()
Resolução
a)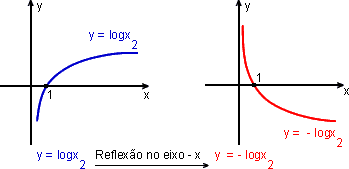
b)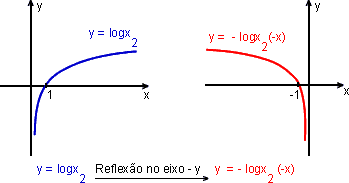
c)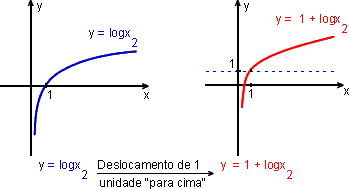
d)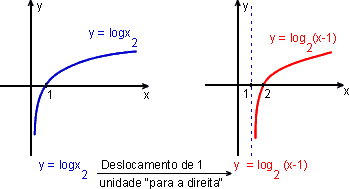
Note que o domínio da função f(x) = 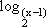 é { x ∈
é { x ∈ 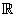 | x – 1 > 0} = { x ∈
| x – 1 > 0} = { x ∈ 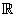 | x > 1}.
| x > 1}.
Propriedades imediatas
|
Propriedade |
Justificação |
|
1. 2. 3. 4. |
b0 = 1 b1 = b bx = bx
|
Exemplos
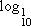 = 0 (1)
= 0 (1) 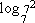 = 2 (3)
= 2 (3)
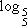 = 1 (2)
= 1 (2) 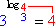 (4)
(4)
As leis dos logaritmos
Sabemos que 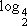 = 2 porque 22 = 4, que
= 2 porque 22 = 4, que 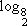 = 3 porque 23 = 8 e que
= 3 porque 23 = 8 e que 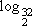 = 5 porque 25 = 32.
= 5 porque 25 = 32.
Note que
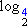 +
+ 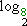 = 2 + 3
= 2 + 3
= 5
= 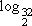
= 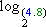
Então,
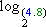 =
= 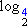 +
+ 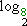 ,
,
isto é, o logaritmo do produto 4 . 8 é a soma dos logaritmos dos fatores. Esse resultado é um caso particular de uma das (três) leis dos logaritmos.
Leis dos logaritimos
Se M e N são positivos, com b > 0 e b ≠ 1, então:
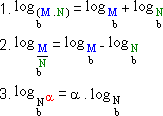
Exemplo
Para os números positivos A, B e C temos
|
|
|
Lei 2 |
|
= |
Lei 1 | |
|
= 3 . |
Lei 3 |
Exercícios
1. Usando as Leis dos Logarítmos desenvolver as expressões.
a) ![]()
b) log (a5 . b7)
c) ![]()
d) ln ![]()
Resolução
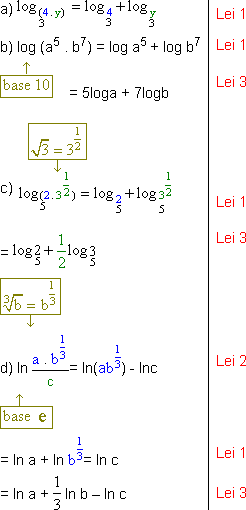
2. Usando as Leis dos Logarítmos calcular cada expressão.
a) ![]()
b) ![]()
c) - ![]() log 27
log 27

Resolução
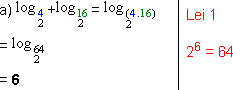
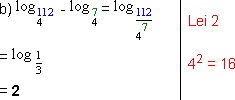
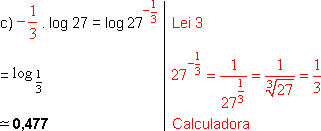
3. Escrever a expressão como um único logarítmo.
a) 2 ![]() +
+ ![]()
![]()
b) ![]()
c) log . (x + 1) + 3 log . x - 2log . (x - 2)
Resolução
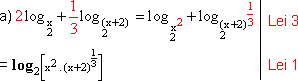
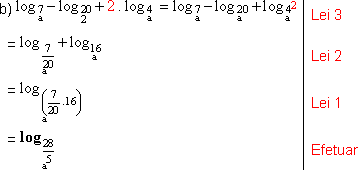
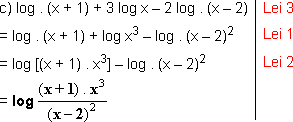
| Erro comum
|
Mudança de base
Se conhecemos o logaritmo de um número em uma base b, podemos determinar esse logaritmo em outra base a. Para isso, usamos a Fórmula de Mudança de Base.
|
Fórmula de mudança de base Se x, b e a são números positivos, b ≠ 1 e a ≠ 1, então
|
Em particular, substituindo x por a na fórmula e lembrando que 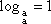 , vem
, vem
|
|
Exemplo
Podemos calcular 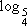 usando os logaritmos decimais.
usando os logaritmos decimais.
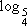 =
= 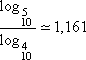

Observação
Podemos escrever a Fórmula de Mudança de Base assim
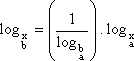

Equações Logarítmicas
Equação logarítmica é aquela na qual ocorre o logarítmico de uma incógnita. Por exemplo,
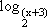 = 4
= 4
Para resolvê-la, nós a reescrevemos na forma exponencial
x + 3 = 24
Daí,
x + 3 = 16
x = 13
Observação
Encontrado um valor para x, é prudente que se faça uma verificação; pode acontecer que tal valor, substituído na equação proposta, faça com que apareça um logaritmo de número negativo; ele deve ser rejeitado.
Propriedade
Para a resolução de equações logarítmicas é útil a propriedade abaixo, que resulta do fato da função logarítmica ser 1 - 1.
|
Propriedade 1 - 1 Para M e N positivos, b > 0 e b ≠ 1, temos: Se |
Exemplo
Se 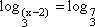 então,
então,
x - 2 = 7
x = 9
Exercícios
1. Resolver a equação 1 + 2 . ![]() = 5.
= 5.
Resolução
Temos:

Cheque a resposta
Para x = ![]() temos
temos
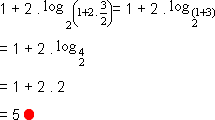
Observação
Quando em uma resposta encontrada colocamos  significa que a verificação foi feita e a raiz é aceitável.
significa que a verificação foi feita e a raiz é aceitável.
2. Resolver a equação ![]() = 2.
= 2.
Resolução
Temos:
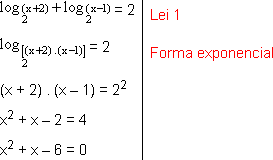
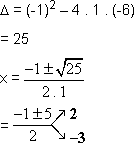
Cheque a resposta
Para x = 2 temos
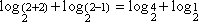
= 2 + 0
= 2 
Para x = - 3 temos
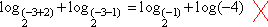
Não definido
3. Resolver a equação log (17x + 2) = 2log6.
Resolução
Temos:
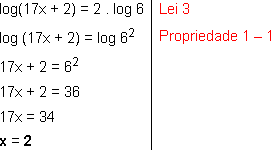
Cheque a resposta
Para x = 2 temos
log(17 . 2 + 3) = log (34 + 2) = log36
= log62 = 2 log6 
4. Resolver a equação (lnx)2 + lnx2 - 3 = 0.
Resolução
Temos:
![]()
Agora, substituindo lnx por y, isto é, fazendo lnx = y, obtemos a equação do 2º grau
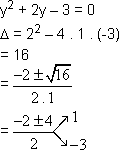
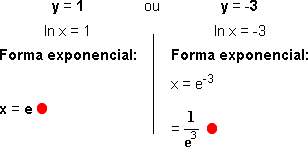
5. Resolver a equação ![]() .
.
Resolução
Como ![]() , temos
, temos
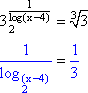
Daí,
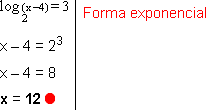
6. Resolver a equação ![]() = 2
= 2
Resolução

Áreas exclusivas para assinantes






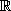 dos números reais, e o conjunto imagem de f é o conjunto I = {y ∈
dos números reais, e o conjunto imagem de f é o conjunto I = {y ∈ 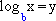 quando
quando 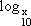
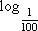
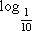
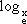
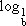 = 0
= 0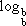 = 1
= 1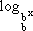 = x
= x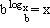
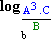 =
= 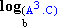 -
- 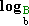
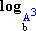 =
= 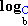 -
- 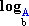 =
= 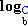 -
- 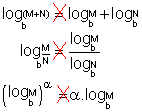
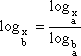
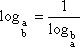
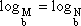 então M = N
então M = N