Fontes de Campo Magnético

O EXPERIMENTO DE OERSTED

Em 1820, o físico dinamarquês Hans Christian Oersted percebeu que uma bússola colocada próxima de um fio conduzindo corrente elétrica, sofria desvios. Isso mostrou que as correntes elétricas também produzem campos magnéticos.

Mais tarde as pesquisas revelaram que todo campo magnético é produzido pelo movimento de cargas elétricas. No caso dos ímãs é o movimento dos elétrons que produz o campo magnético. Hoje sabemos que:

a) Uma carga elétrica em repouso produz apenas campo elétrico.

b) Uma carga elétrica em movimento produz dois campos: um campo elétrico e um campo magnético.

O cálculo do campo magnético produzido pelas cargas em movimento é em geral bastante complexo. Assim analisaremos apenas alguns casos particulares.

FIO RETILÍNEO

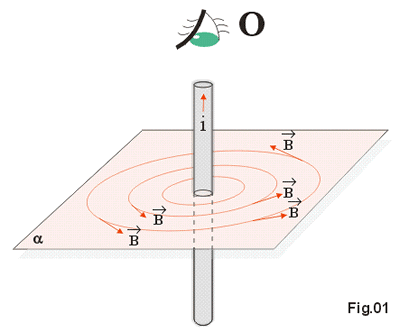
Consideramos um fio retilíneo e "longo", percorrido por uma corrente de intensidade i. Em volta do fio existe um campo magnético tal que, próximo do fio as linhas de campo são circunferências (Fig. 1) cujo centro está no fio. Na Fig. 1 as linhas circulares estão contidas no plano    o qual é perpendicular ao fio.

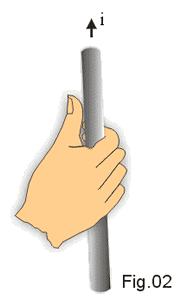
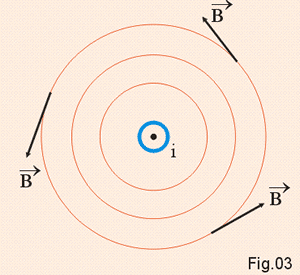
Para determinarmos o sentido do campo magnético usamos a regra da mão direita (Fig. 2). Envolvemos o fio com a mão direita, de modo que o polegar aponte no sentido da corrente; a curvatura dos outros dedos nos dá o sentido de . Para o observador O da Fig. 1, as linhas de campo têm o aspecto da Fig. 3.

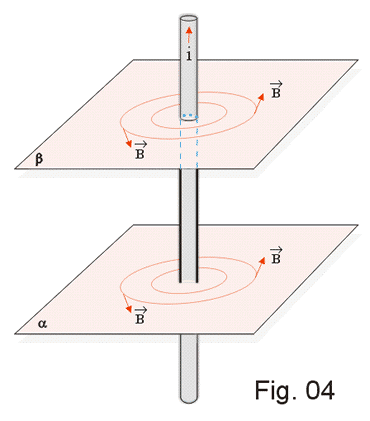
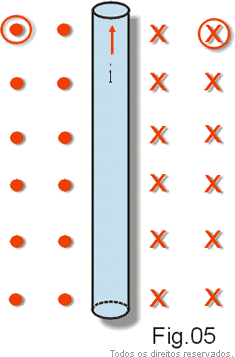
Na Fig. 4 representamos algumas linhas de campo situadas em dois planos distintos α e β. Representando o campo no plano do papel (Fig. 5), o campo "entra" no papel à direita do fio (símbolo ) e sai do papel à esquerda do fio (símbolo ).

 O módulo de em um ponto é dado por:

    (I)

onde d é a distância do ponto ao fio e μo é uma constante, denominada permeabilidade do vácuo, cujo valor do SI é μo = 4π. 10^-7. Da equação I tiramos:

Assim:

unidade de

Portanto:

ESPIRA CIRCULAR

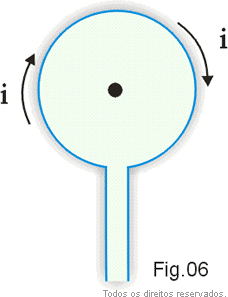
Na Fig. 6 representamos um fio dobrado em forma de espira circular, percorrido por uma corrente de intensidade i.

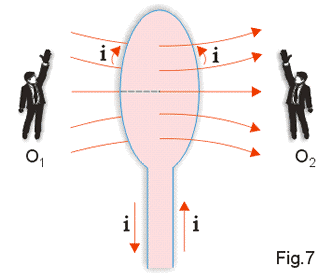
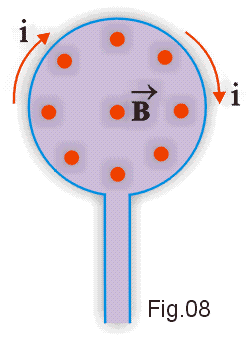
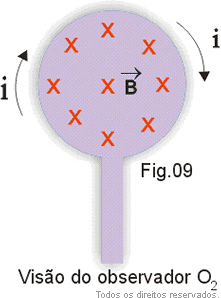
 Na Fig. 7 apresentamos uma visão em perspectiva da espira, com as linhas do campo magnético produzido. O sentido do capo pode ser obtido pela regra da mão direita. O observador O₁ da Fig. 7 vê o campo "entrando" no plano da espira (Fig. 8) e o observador O₂ vê o campo "saindo" do plano da espira (Fig. 9).).

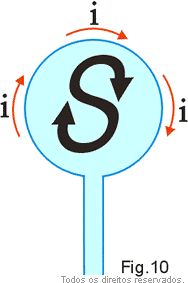
 Em analogia com os ímãs, a face por onde "saem" as linhas é chamada de face norte (Fig. 10) e a face por onde "entram" as linhas é chamada de face sul (Fig. 11). Observe que as extremidades da S e do N nos dão o sentido da corrente.

                   

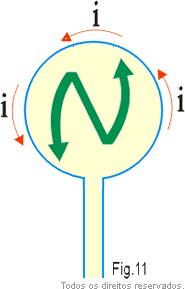
Essa atribuição de polaridade às faces, nos ajuda a decidir o tipo de força que ocorre entre duas espiras ou entre uma espira e um ímã.

Consideremos duas espiras circulares, percorridas por correntes elétricas, colocadas face a face, isto é, com seus planos paralelos, observamos que:

a) duas faces norte se repelem

b) duas faces sul se repelem

c) uma face norte e uma face sul se atraem

CAMPO NO CENTRO DA ESPIRA

No centro da espira, a intensidade do campo magnético é dada por:

    (II)

onde R é o raio da espira.

BOBINA CHATA

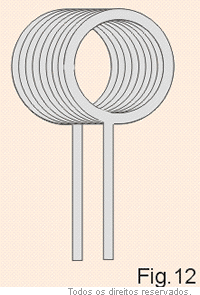
Se enrolarmos o condutor de modo a obtermos várias espiras circulares de mesmo raio e superpostas compactamente, como ilustra a Fig. 12, obteremos o que se chama bobina chata. No centro da bobina a intensidade do campo é:

    (III)

onde N é o número de espiras.

SOLENOIDE

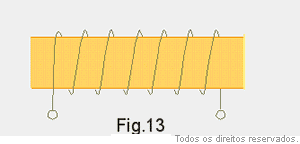
Na Fig. 13 representamos um fio enrolado de modo que temos várias espiras circulares, uma ao lado da outra. Esse objeto é denominado solenoide ou bobina longa.

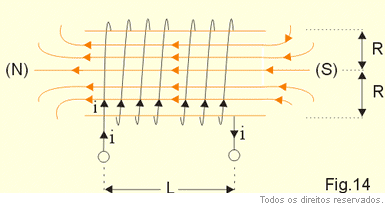
Quando o comprimento do solenoide (L) é bem maior do que o raio das espiras (R) e o solenoide é percorrido por corrente elétrica forma-se um campo magnético cujas linhas têm o aspecto da Fig. 14; no interior do solenoide o campo é aproximadamente uniforme.

 

A intensidade do campo magnético no interior do solenoide é dada por:

     (IV)

onde N é o número de espiras.

O quociente é o número de espiras por unidade de comprimento. Se representarmos esse quociente por n, isto é, n = , a fórmula IV pode ser escrita:

B = μo n i    (IV)

A extremidade do solenoide por onde "saem" as linhas de campo (Fig. 14) comporta-se como um polo norte e a extremidade por onde "entram" as linhas, comporta-se como um polo sul; o campo produzido por um solenoide é semelhante ao campo produzido por um ímã em forma de barra.

CAMPO MAGNÉTICO DE UM ÍMÃ

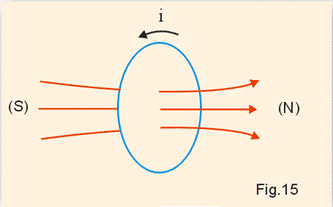
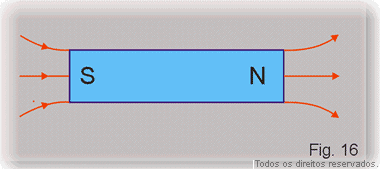
O movimento dos elétrons no interior da matéria, produz campo magnético. O campo magnético produzido por um elétron é semelhante ao campo produzido por uma espira circular (Fig. 15), isto é, cada elétron produz um campo semelhante ao de um minúsculo ímã (Fig16) denominado ímã elementar.

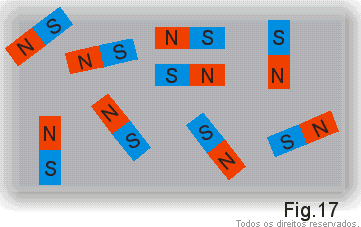
Nos corpos macroscópicos temos um número muito grande de elétrons que produzem campos magnéticos em todas as direções (Fig. 17), de modo que o efeito médio é nulo, isto é, em geral os corpos não apresentam efeitos magnéticos.

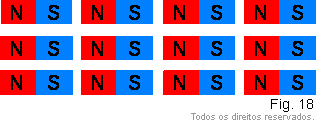
Há, porém, alguns matérias que, na presença de um campo magnético, têm seus ímãs elementares aproximadamente alinhados (Fig. 18) transformando-se momentaneamente em ímã. É o caso do ferro, que é atraído pelos ímãs.

Em geral, com a retirada do campo magnético externo os ímãs elementares desses materiais voltam à desordem inicial, perdendo seu efeito magnético. No entanto há alguns materiais que, após a retirada do campo externo mantêm seus ímãs elementares aproximadamente alinhados, transformando-se em ímãs permanentes.

Os materiais que têm comportamento semelhante ao do ferro são chamados de ferromagnéticos. Como exemplos podemos citar o cobalto, o níquel e o gadolínio.

ELETROÍMÃ

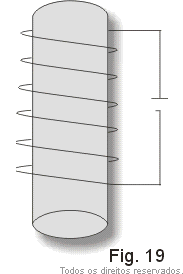
Colocando-se um núcleo de ferro no interior de um solenoide, observamos que o campo magnético fica muito mais intenso (Fig. 19).

Tal objeto é denominado eletroímã e é usado em aparelhos tais como campainhas e guindastes magnéticos.

PONTO CURIE

Consideramos um ímã permanente. Aquecendo-se esse corpo, aumenta a agitação das moléculas. Desse modo, atingindo uma certa temperatura, a agitação pode desfazer o alinhamento dos ímãs elementares. Essa temperatura é denominada ponto de Curie. No caso do ferro, o ponto Curie é 770º C.

FORÇA ENTRE CONDUTORES PARALELOS

Consideremos dois condutores retos, longos e paralelos como ilustra a Fig.20. Suponhamos que os fios sejam percorridos por correntes elétricas de mesmo sentido e intensidades i₁ e i₂.

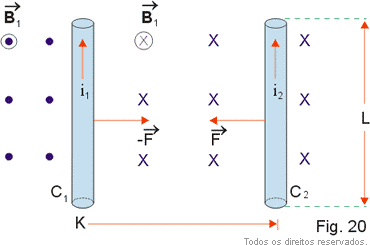
Na figura representamos o campo produzido pela corrente i₁ ( ₁ ). A intensidade desse campo é dada por:

O condutor C₂ sofre a ação do campo ₁. Assim a força exercida sobre o condutor C₂ é dada por:

Aplicando a regra da mão esquerda percebemos que nesse caso as forças são de atração. Quando os fios são percorridos por correntes de sentidos opostos ( Fig.21) existe entre eles um par de forças de repulsão.

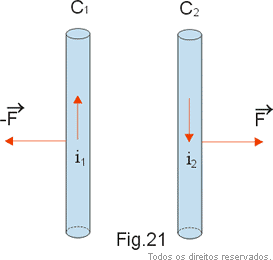
A fórmula VI foi obtida considerando o campo produzido por C₁, atuando sobre C₂. O resultado seria o mesmo se considerássemos o campo produzido por C₂ atuando em C₁.

DEFINIÇÃO DO AMPÈRE

No Sistema Internacional, a umidade elétrica de base não é o coulomb mas sim o ampère; o coulomb é definido a partir do ampère, usando a equação:

Assim, existe um procedimento padrão para obter-se a corrente de intensidade 1 ampère. Esse procedimento a equação VI; considerando i₁ = i₂ = i:

Fazendo i = 1A e d = 1m temos:

A partir da equação VII define - se o ampère:

O ampère é a intensidade de uma corrente constante que, estabelecida em dois condutores retos, paralelos e longos, separados por uma distância de 1 metro, no vácuo faz parecer entre eles, força magnética de intensidade por metro.