Energia Mecânica

A energia potencial gravitacional, a energia potencial elástica e a energia cinética são formas de energia mecânica.

E_p.grav. = ± mgh

Energia Potencial Gravitacional

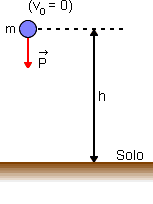
Na Fig. 1 representamos uma partícula de massa m a uma altura h acima do solo. Se a partícula tem nesse ponto velocidade v_o = 0, não possui energia cinética. No entanto, se abandonarmos a partícula nessa posição, ela descerá, sob a ação do peso, ganhando energia cinética. Dizemos então que a uma altura h, a partícula possui uma energia potencial (E_p) que é igual ao trabalho realizado pela força peso durante a descida:

Essa energia potencial é chamada energia potencial gravitacional.

Energia Potencial Elástica

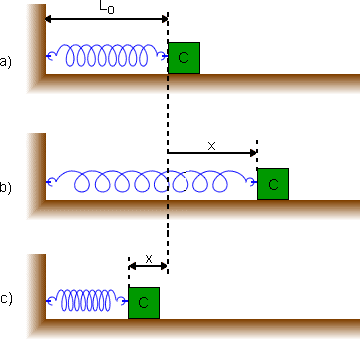
Na Fig. a representamos uma mola ideal de comprimento natural L_o presa a um corpo C ; nessa situação o sistema está em equilíbrio.

Se esticarmos a mola (Fig.b) ou se a comprimirmos (Fig. c), provocando uma deformação x, podemos dizer que a mola adquire uma energia potencial.

A energia potencial armazenada é:

K = constante elástica da mola (N/m ou N/cm)

x = deformação (m ou cm)

Essa energia é chamada de energia potencial elástica.

Exemplo

Uma mola de comprimento natural L_o = 1,5m e constante elástica k = 200 N/m foi esticada até que seu comprimento passasse a L = 1,7 m. Calcule a energia potencial armazenada na mola.

Resolução

A deformação da mola é a diferença entre seu comprimento final e o comprimento natural:

x = L - Lo = 1,7 m - 1,5 m = 0,2 m

Assim, a energia potencial da mola é:

E_p = 4 joules = 4 J

ENERGIA MECÂNICA

Quando um corpo está em movimento, a soma da energia cinética (E_c) com a energia potencial (E_p) é chamada de energia mecânica (E_m):

Exemplo 1

Em uma região em que g = 10 m/s², um corpo de massa m = 4,0 kg cai em queda livre, de modo que quando sua altura em relação ao solo é h = 3,0 m, sua velocidade é 5,0 m/s.

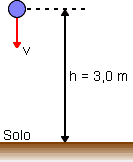
Calcule a energia mecânica desse corpo (em relação ao solo), nesse momento.

Resolução

A energia cinética (E_c) é dada por:

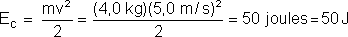
A energia potencial gravitacional em relação ao solo é:

E_p = mgh = (4,0 kg) (10 m/s²) (3,0 m) = 120 joules = 120 J

A energia mecânica (E_m) é a soma da energia cinética com a energia potencial:

E_m = E_c + E_p = 50 J + 120 J = 170 J

Conservação da energia mecânica

Suponhamos que um corpo esteja em movimento de modo que, entre as forças que atuam sobre ele, a única que realiza trabalho seja o peso. Nesse caso pode-se demonstrar que, durante o movimento, a energia mecânica é constante; se uma das energias aumenta, a outra diminui, de modo que a soma se mantém constante. Diz-se também que, nesse caso, a energia mecânica é conservada e, por esse motivo, o peso é chamado de força conservativa. Outros exemplos de forças conservativas são força da gravidade, força elástica, etc.

Nos sistemas conservativos tem-se:

E_c + E_p = E_{mec. total} = constante

Para cada força conservativa, existe em correspondência uma energia potencial. Se as únicas forças que realizam trabalho são as forças conservativas, a energia mecânica fica constante, isto é, a soma da energia cinética com todas as potenciais, se mantém constante.

Quando além das forças conservativas, existem forças de atrito, estas ocasionam uma diminuição da energia mecânica e essa perda é transformada principalmente em calor. A energia mecânica perdida é também, chamada de energia dissipada.

Sistemas Dissipativos

Quando existe atrito, a energia mecânica não é conservada porque parte ou toda se dissipa na forma de calor.

Conservação da Energia Total

"A energia pode transformar-se de uma forma para outra, não podendo ser criada ou destruída".

Avalie a aula