Corrente elétrica
- Home
- Corrente Elétrica
CARGA ELÉTRICA
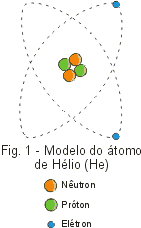
A matéria é formada por átomos, os quais por sua vez são formados por três tipos de partículas: prótons, elétrons e nêutrons. Os prótons e nêutrons agrupam-se no centro do átomo formando o núcleo. Os elétrons movem-se em torno do núcleo. Num átomo o número de elétrons é sempre igual ao número de prótons. Às vezes um átomo perde ou ganha elétrons; nesse caso ele passa a se chamar íon.
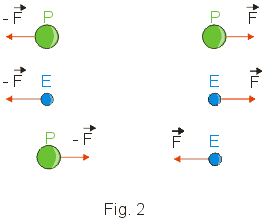
A experiência mostra que: (Fig. 2)
I - Entre dois prótons existe um par de forças de repulsão;
II - Entre dois elétrons existe um par de forças de repulsão;
III - Entre um próton e um elétron existe um par de forças de atração;
IV - Com os nêutrons não observamos essas forças.
Dizemos que essas forças aparecem pelo fato de elétrons e prótons possuírem carga elétrica. Para diferenciar o comportamento de prótons e elétrons dizemos que a carga do próton é positiva e a carga do elétron é negativa. Porém, como em módulo, as forças exercidas por prótons e elétrons são iguais, dizemos que, em módulo, as cargas do próton e do elétron são iguais. Assim, chamando de qp a carga do próton Ea carga do elétron temos:
| qE | = | qp|
qE = - qp
O mais natural seria dizer que a carga do próton seria uma unidade. No entanto, por razões históricas, pelo fato de a carga elétrica ter sido definida antes do reconhecimento do átomo, a carga do próton e a carga do elétron valem:
qp = + 1,6 . 10-19 coulomb = 1,6 . 10-19 C
qE = - 1,6 . 10-19 coulomb = -1,6 . 10-19 C
onde o coulomb (C) é a unidade de carga elétrica no Sistema Internacional. A carga do próton é também chamada de carga elétrica elementar (e). Assim:
qp = + e = + 1,6 . 10-19 C
qE = - e = - 1,6 . 10-19 C
Como o nêutron não manifesta esse tipo de força, dizemos que sua carga é nula.
CONDUTORES E ISOLANTES
Chamamos de condutor elétrico um material que permite a movimentação de cargas elétricas. Os metais são bons condutores pelo fato de existirem os elétrons livres, que são os elétrons mais afastados dos núcleos. Eles estão fracamente ligados aos núcleos e assim movem-se com facilidade. Quando dissolvemos um sal ou um ácido em água, esta provoca a dissociação das moléculas em íons, os quais podem se movimentar. Portanto uma solução iônica também é um condutor.
Chamamos de isolante, um material em que a movimentação de cargas elétricas é muito difícil. Como exemplo temos a borracha, o vidro, a ebonite.
INTENSIDADE DE CORRENTE
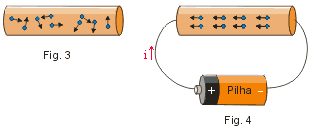
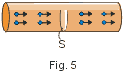
Consideremos um fio metálico. Normalmente os elétrons livres movem-se caoticamente em todas as direções (Fig. 3). No entanto, quando ligamos os extremos do fio aos terminais de uma pilha (Fig. 4) ou bateria, os elétrons livres adquirem um movimento aproximadamente ordenado, formando o que chamamos de corrente elétrica.
No estudo da eletrostática e do magnetismo veremos que um elétron movendo-se num sentido, produz o mesmo efeito que um próton movendo-se no sentido oposto. Assim, pelo fato de no século XIX, os estudiosos acreditarem que eram as cargas elétricas positivas que se movimentavam, ainda hoje indicamos o sentido da corrente elétrica (i) como oposto ao movimento dos elétrons como indicamos na Fig. 4; esse sentido é chamado de sentido convencional da corrente elétrica. Assim, dizemos que a corrente convencional sai do polo positivo da pilha (+) e entra pelo polo negativo da pilha (-).
Em um fio cilíndrico consideremos uma seção transversal S. Suponhamos que, num intervalo de tempo ![]() , passa por S uma carga elétrica Q. A intensidade média da corrente (im) é definida por:
, passa por S uma carga elétrica Q. A intensidade média da corrente (im) é definida por:
![]()
Quando a velocidade dos elétrons não é constante, definimos uma intensidade instantânea de modo análogo ao que fizemos com a velocidade instantânea:
![]()
No entanto, neste curso, só consideraremos casos em que os elétrons movem-se com velocidade constante e, assim, a intensidade média é igual à intensidade instantânea.
![]()
No Sistema Internacional, a unidade de intensidade de corrente é o ampère (A):
![]()
Exemplo 1
Pela seção reta de um fio, em um intervalo de tempo ![]() = 3,0 segundos, passam 12 . 108 elétrons. Calcule a intensidade de corrente.
= 3,0 segundos, passam 12 . 108 elétrons. Calcule a intensidade de corrente.
Resolução
Sendo N o número de elétrons que passam pela seção S no intervalo de tempo ![]() temos:
temos:
N = 12 . 108
Sabemos que o módulo da carga de um elétron é igual à carga elementar e:
e = 1,6 . 10-19 C
Assim, sendo Q o módulo da carga que passa por S, no intervalo de tempo ![]() , temos:
, temos:
|Q| = N . e
Assim:
![]()
i = 6,4 . 10-11C/s = 6,4 . 10-11 A
Muitas vezes teremos correntes de intensidades muito pequenas e usaremos submúltiplos do ampère que podem ser expressados usando os prefixos do SI.
Assim, por exemplo:
1mA = 1 miliampère = 10-3 A
1![]() A = 1 microampère = 10-6 A
A = 1 microampère = 10-6 A
1nA = 1 nanoampère = 10-9 A
1pA = 1 picoampère = 10-12 A
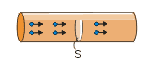
Gráfico de i x t
Na Fig. 6 representamos o gráfico de i em função do tempo (t) para o caso em que a corrente tem intensidade constante.
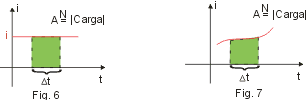
Sabemos que:
![]()
Assim, percebemos que, no caso da Fig. 6, a área da figura sombreada (A) é numericamente igual ao módulo da carga que passa pela seção reta do fio num intervalo de tempo
![]() :
: ![]()
Para o caso em que a intensidade de corrente é variável (Fig. 7), é possível demonstrar que a propriedade continua válida:
![]()
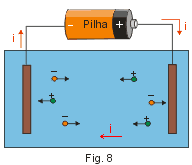
CORRENTES IÔNICAS
Há substâncias que ao se dissolverem em água têm suas moléculas dissociadas em íons (como por exemplo um sal ou um ácido). Assim se introduzirmos na solução duas placas metálicas ligadas aos terminais de uma pilha (Fig. 8) ou bateria, haverá um movimento de íons positivos num sentido e íons negativos no sentido oposto.
Suponhamos que:
![]()
Como o movimento das cargas negativas num sentido é equivalente ao movimento de cargas negativas no sentido oposto, a intensidade total de corrente (i) é dada por:
i = ( i + ) + ( i - )
Sumário
- Carga elétrica- Condutores e isolantes
- Intensidade de corrente
i. Gráfico de i x t
- Correntes iônicas
Áreas exclusivas para assinantes





