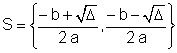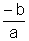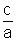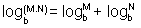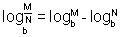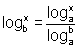Conjuntos Numéricos - Operações com Conjuntos
- Home
- Conjuntos Numéricos Operações Com Conjuntos
Conjuntos Numéricos - Operações com Conjuntos
Os números racionais
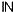 = { 0, 1, 2, 3, ...} é o conjunto dos números naturais.
= { 0, 1, 2, 3, ...} é o conjunto dos números naturais.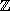 = {..., -3, -2, -1, 0, 1, 2, 3, ...} é o conjunto dos números inteiros.
= {..., -3, -2, -1, 0, 1, 2, 3, ...} é o conjunto dos números inteiros.- é racional um número que pode ser escrito como um quociente entre dois inteiros; assim, se p e q são números inteiros e
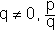 é um número racional.
é um número racional.
Por exemplo
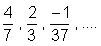
são números racionais.
Os números inteiros são também números racionais; eles podem ser escritos como um quociente entre dois inteiros:
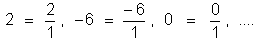
Um número racional pode, ainda, ser escrito na forma decimal, como por exemplo:
|
3,7 |
Note que nos três primeiros números, a representação decimal "termina" e é simples escrever frações correspondentes que os representam:
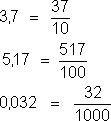
Para os dois outros exemplos, a representação decimal "não termina", é um grupo de algarismos que repete-se uma infinidade de vezes: são as dízimas periódicas.
Podemos sempre determinar uma fração que é igual a uma dízima periódica qualquer, isto é, uma dízima periódica representa efetivamente um número racional.
Por exemplo, vamos obter uma fração que gera a dízima 0,222...
Temos:
x = 0,222... (1)
10 . x 2,222 ....(2)
Fazemos a subtração (2) - (1) , obtendo
10 x - x = (2,222....) - (0, 222....),
donde
9 x = 2
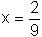
Os números reais
Certos números como 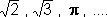 não podem ser escritos como um quociente entre inteiros. Esses números não são racionais; eles são chamados números irracionais.
não podem ser escritos como um quociente entre inteiros. Esses números não são racionais; eles são chamados números irracionais.
Um número irracional pode ser escrito na forma decimal; por exemplo:
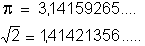
Essa representação decimal apresenta uma infinidade de algarismos e não é periódica.
O conjunto constituído pelos números racionais e pelos números irracionais é denominado conjunto dos números reais, e é representado com a letra 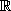 .
.
A reta numérica
Podemos nos utilizar de uma reta para representar o conjunto 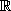 dos números reais.
dos números reais.
Para construirmos essa representação, sobre uma reta selecionamos um ponto O - chamado origem - para representar o número zero; depois, "à direita" da origem marcamos um ponto U para representar o número 1. A distância entre O e U é então a unidade de comprimento.
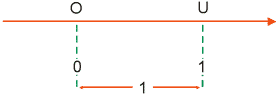
Agora, observe que os números reais, não nulos, dividem-se em dois tipos distintos: os números positivos e os números negativos. Identificamos um número positivo a com o ponto da reta que está à distância a unidades "à direita" da origem. Se a é negativo, então o identificamos com o ponto localizado - a unidades "à esquerda" da origem.
A figura abaixo mostra o resultado dessa identificação.
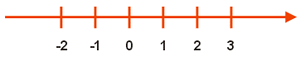
A reta sobre a qual construímos uma representação para 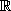 é denominada reta numérica ou reta real.
é denominada reta numérica ou reta real.
A identificação entre os números reais e os pontos de uma reta estabelece que cada número real corresponde a exatamente um ponto da reta e, inversamente, cada ponto da reta numérica corresponde a um único número real.
O ponto A identificado com o número real a é chamado gráfico de a; diz-se também que o ponto A tem abscissa a
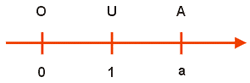
Se A tem abcissa a, escrevemos:
A (a)
Intervalos
Na reta real, um segmento ou uma semirreta chamam-se intervalos. Há diferentes maneiras para representá-los, como descrevemos abaixo:
Sejam, então, a e b reais, com a < b; temos:
|
Notação de conjunto |
Notação de intervalo |
Gráfico |
|
|
[ a ; b ] |
|
|
|
] a ; b [ |
|
|
|
] a ; b ] |
|
|
|
[ a ; b [ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fica convencionado, também, que escreveremos:
|
|
5. Inclusão
Vimos que todo número inteiro é um número racional; por exemplo, o inteiro 21 é racional pois pode ser escrito na forma 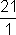 , de um quociente entre inteiros. Em outras palavras:
, de um quociente entre inteiros. Em outras palavras:
- todo elemento do conjunto
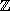 é um elemento do conjunto
é um elemento do conjunto 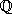
Traduzimos uma tal situação dizendo que 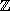 está contido no conjunto
está contido no conjunto ![]() , e escrevemos
, e escrevemos ![]()

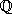 .
.
De um modo geral, temos:
|
Definição Todos os conjuntos A e B, diz -se que A está contido em B (ou que A é um subconjunto de B), e indicamos A |
Note que : 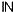

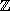

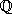

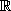
Intersecção e união
Você se lembra de que um círculo D é o conjunto de pontos interiores a uma circunferência C mais a própria circunferência.
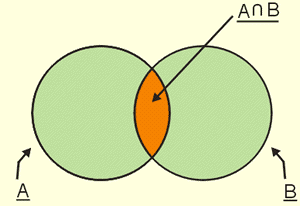
Na figura representamos dois círculos D1 e D2 e colorimos os pontos comuns a D1 e D2.
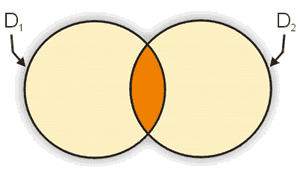
Esse conjunto (de pontos), assim destacado, chama-se intersecção de D1 e D2; o que se nota com D1  D2 e que se lê : "D1 inter D2."
D2 e que se lê : "D1 inter D2."
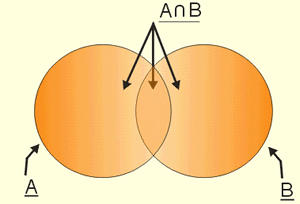
Podemos também considerar o conjunto dos pontos que pertencem ao menos a um dos dois conjuntos, isto é, pertencem a D1, pertencem a D2, pertencem a D1  D2:
D2:
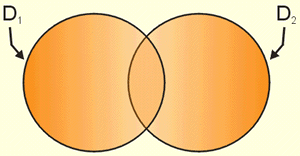
Diz-se que esse conjunto é constituído pelos pontos que pertencem a D1 ou a D2. é chamado de união de D1 e D2; o que se nota com D1  D2,que se lê: "D1 união D2."
D2,que se lê: "D1 união D2."
|
Definição Sejam os conjuntos A e B.
A intersecção desses conjuntos é o conjunto de todas os elementos comuns a A e a B. A intersecção de A e B é notada com A |
|
Definição Sejam os conjuntos A e B.
A união desses conjuntos é o conjunto de todos os elementos que pertencem a A ou a B ( a pelo menos um dos conjuntos A e B ) A união de A e B é notada com A |
Fatoração
1. A forma fatorada dos números naturais
Se um número natural a divide exatamente um segundo número natural b, a é um fator de b. Por exemplo, 3 divide 12, e é então um fator de 12.
Note que os fatores de 12 são:
- 1, 2, 3, 4, 6, 12
pois cada um deles divide 12 exatamente.
Fatorar um número é escrevê-lo como o produto de outros números naturais. Se cada um desses fatores é um número primo, o número natural diz-se fatorado em um produto de fatores primos.
Exemplo
60 = 22 . 3. 5
140 = 22 . 5. 7
180 = 22 . 32. 5
O maior número natural que divide 60, 140 e 180 denomina-se máximo divisor comum desses três números. Indica-se:
- MDC (60, 140, 180)
Note que 60, 140 e 180 têm dois fatores 2 e um fator 5, comuns, seu MDC é 22 . 5 = 20
Monômios algébricos como 3 p2.q.r, 6p3.q2.r e 9p4.q3 também têm MDC:
3 p2q r = 3.p.p.q.r
6 p3q2r = 3.2.p.p.p.q.q.r
9 p4q3 = 3.3.p.p.p.p.q.q.q.
Cada monômio tem um fator 3, dois fatores p e um fator q, comuns, então, o MDC dos monômios é:
3. p2.q
Soma e diferença de cubos
Para fatorarmos uma soma ou diferença de dois cubos, usamos os seguintes resultados:
(a + b) . (a2 - ab + b2) = a3 + b3
(a - b) . (a2 + ab + b2) = a3 - b3
Para verificarmos, por exemplo, a primeira das fórmulas, efetuamos o produto indicando no seu primeiro membro.
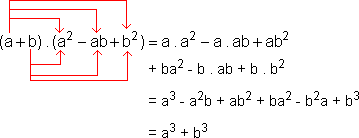
|
Fatoração de uma soma ou diferença de cubos a3 + b3 = (a + b) . (a2 - ab + b2) a3 - b3 = (a - b) . (a2 + ab + b2) |
Exemplos
a3 + 8 = a3 + 23 = (a + 2) . (a2 - a2 + 22)
= (a + 2) . (a2 + 2a + 4)
27 x3 -64 y3 = (3x)3 - (4y)3
= (3x - 4y) . [(3x)2 + 3x . 4y + (4y)2]
= (3 x - 4 y) . (9x2 - 12 xy + 16 y2)
Equação do 1º grau
Equação do tipo a x + b = 0, x 

Se a 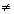 0, a equação se escreve:
0, a equação se escreve:
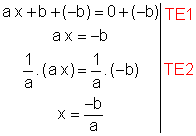
Note que a equação é do 1º grau e admite uma única solução: 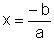
Se a = 0, a equação se escreve:
x = - b.
Se b 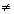 0, a equação não admite soluções.
0, a equação não admite soluções.
Se b = 0, toda x, x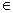
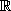 , é solução da equação.
, é solução da equação.
|
Resumo - equação a x+ b = 0, x
|
Equação do 2º grau
1. Trinômio do 2º grau
|
Definição Um trinômio do 2º grau, na variável x é uma expressão da forma f (x) = a x2 + b x + c, onde a,b e c são números reais, e a |
2. Forma canônica do trinômio do 2º grau
Seja o trinômio f (x) = a x2 + b x + c, a 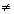 0. Temos :
0. Temos :
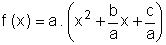 (a em evidência)
(a em evidência)
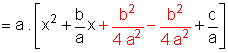
E, sendo 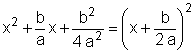 , vem:
, vem:
|
|
que é a forma canônica do trinômio do 2º grau.
3. Equação do 2º grau: a x2+ b x + c = 0
Fazendo b2 - 4 ac =  , a equação a x2+ b x + c = 0 é equivalente a:
, a equação a x2+ b x + c = 0 é equivalente a:
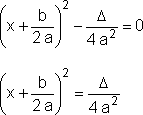
Então, se  < 0, a equação não admite soluções (um quadrado é não negativo).
< 0, a equação não admite soluções (um quadrado é não negativo).
Se  = 0, a equação admite uma única solução:
= 0, a equação admite uma única solução:
x = -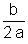
Se  > 0, a a equação admite duas soluções:
> 0, a a equação admite duas soluções:
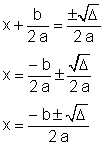
|
Teorema Seja a equação a x2 + b x + c = 0, com a Seja S seu conjunto - solução Torna-se
|
4. Fatoração do trinômio a x2 + b x + c
Utilizando a forma canônica,
a x2 + b x +c = a .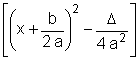 ,
,
temos:
 , o resultado é evidente:
, o resultado é evidente:
a x2 + b x + c = a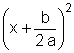
 > 0, escrevendo
> 0, escrevendo
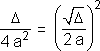 ,
,
fazemos aparecer uma diferença de dois quadrados:
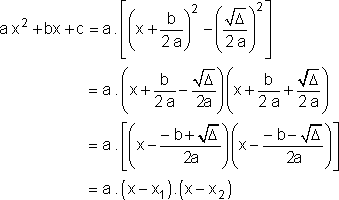
|
Teorema Sejam o trinômio do 2º grau ax2 + b x + c e Se a x2 + b x + c = a (x -x1)(x - x2) Se a x2 + b x + c = (x - x0)2 |
Relações entre as raízes e o coeficiente de uma equação do 2º grau
1. Propriedade
Seja a equação do 2º grau a x2 + b x + c = 0, cujas raízes são x1 e x2. Temos:
x1 = 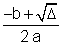 e x2 =
e x2 = 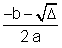
Então,
S = x1 + x2 = 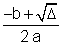 +
+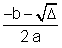 =
=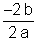 =
=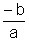
P = x1 . x2 = 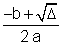 .
.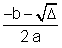
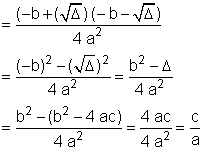
|
Teorema Quando a razão do 2º grau a x2 + b x + c = 0 admite as raízes x1 e x2, sua soma e seu produto são dados por S = x1 + x2 = S = x1. x2 = |
Exemplos
1. Na equação 2 x2 + 3 x - 17 = 0, a soma e o produto das raízes são, respectivamente
S = 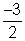
P = 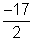
2. Seja a equação 2 x2 -7 x + 5 = 0.
A relação 2 -7 +5 =0 mostra que x1 = 1 é raiz da equação. A outra raiz x2, verifica a condição 1 . x2 = 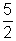 , donde, x2 =
, donde, x2 = 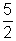 .
.
2. Problema
Sejam S e P dois números reais dados. Existem dois números reais cuja soma é S e cujo produto é P? Se existem, como calculá-los?
Temos:
(x - x1) . (x -x2) = x2 - (x1 + x2) . x + x1 . x2
Note que os raios x1 e x2 são as raízes da equação (x - x1) . (x - x2) = 0, e portanto, são as raízes da equação x2 - (x1 + x2) . x + x1 . x2 = 0. Daí,
- Se x1 + x2 = S e x1 . x2 = P, então x1 e x2 são necessariamente as raízes da equação x2 - S . x + P = 0.
- Se x1 e x2 são as raízes de x2 - Sx + P = 0, então pelo teorema anterior, x1 + x2 = S e x1 . x2 = P.
|
Teorema Dois números reais têm por soma S e por produto P, se e somente se, eles são as raízes da equação x2 - S . x + P = 0 |
O cálculo do discriminante da equação x2 - S . x + P = 0,
 = S2 - 4P,
= S2 - 4P,
mostra que:
Existem dois números reais de soma S e de produto P se e somente se
S2 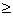 4P
4P
Exemplos
1. Determine, se existem, dois números cuja soma é 4 e cujo produto é 1.
Resolução
Os números procurados são as raízes da equação
x2 - 4x + 1 = 0
Temos  = 16 - 4 = 12 (então, os números existem...)
= 16 - 4 = 12 (então, os números existem...)
E, sendo  = 4.3, isto é,
= 4.3, isto é, 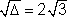 , os números desejados são
, os números desejados são
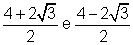 ,
,
ou,
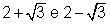
3. Problema
Vamos formar uma equação do 2º grau que tenha como raízes os reais x1 e x2, dados.
Calculamos a soma e o produto de x1 e x2; obtemos:
x1 + x2 = S
x1. x2 = P
Então x1 e x2 são as raízes da equação
x2 - S. x + P = 0
|
Teorema Dados os reais x1 e x2, uma equação cujas raízes são x1 e x2 é x2 - S. x + P = 0, onde S = x1 + x2 e P = x1. x2. |
Exemplos
1. Formar uma equação do 2º grau raízes são 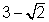 e
e 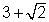 .
.
Resolução
Temos:
S = (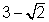 ) + (
) + (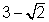 ) = 6
) = 6
P = (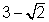 ) . (
) . (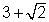 ) =
) = 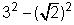 = 9 - 2 = 7
= 9 - 2 = 7
Então, a equação desejada é
x2 - 6x + 7 = 0
A regra de três
Quando y varia diretamente com x a equação y = kx é equivalente a
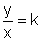
Então se os pares (x1; y1) e (x2; y2) satisfazem y = kx, então cada uma das razões 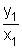 e
e 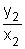 será igual a k:
será igual a k:
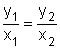
Essa proporção pode ser utilizada para resolver problemas de variação direta, quando não se requer a constante de proporcionalidade - é a regra de três.
O domínio da composta
Dadas as funções f e g, gof é uma função que se diz composta de g e f, definida por
(gof) (x) = g (f (x))
O domínio de gof é o conjunto de todos os x que pertencem ao domínio de f tais que f(x) pertence ao domínio de g
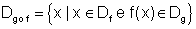
Exemplo
Dadas as funções f e g por
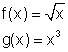 ,
,
vamos determinar o domínio de g o f.
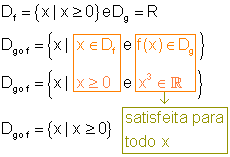
Demonstrações das leis dos logaritmos
Sejam M e N positivos, com b > 0 e b 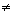 1.
1.
Vamos fazer
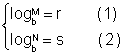
Passando para forma exponencial, temos
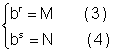
LEI - 1
Multiplicando membro a membro as equações ( 3 ) e ( 4 )
M . N = br . bs = br + s
Passando esta equação para a forma logarítmica vem
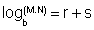
Daí, das equações ( 1 ) e ( 2 ) resulta
|
|
LEI - 2
Dividindo membro a membro as equações ( 3 ) e ( 4 )
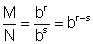
Passando esta equação para a forma logarítmica vem
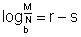
Daí, usando as equações ( 1 ) e ( 2 ) resulta
|
|
LEI - 3
Vamos fazer
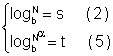
Passando para a forma exponencial, temos
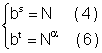
Substituindo ( 4 ) em ( 6 ), vem
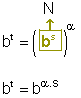
Daí,
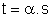
Usando as equações ( 5 ) e ( 2 ) resulta
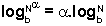 |
Fórmula da Mudança de Base
Suponha que dado 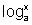 e desejamos
e desejamos 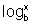
Seja
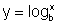
Passando para a forma exponencial vem
by = x
Tomando logaritmo na base a de ambos os membros
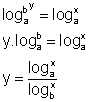
Mas,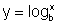 ; então
; então
|
|
Sumário
- Os números racionais- Os números reais
- A reta numérica
- Intervalos
- Inclusão
- Intersecção e união
- Fatoração
- Soma e diferença de cubos
- Equação do 2º grau
- Relações entre as raízes e o coeficiente de uma equação do 2º grau
- A regra de três
- O domínio da composta
- Demonstrações das leis dos logarítmos
Áreas exclusivas para assinantes






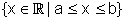
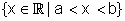
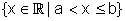
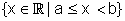
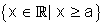
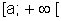
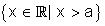
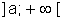
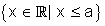
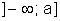
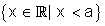
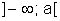
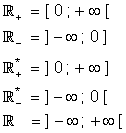
 B.
B.

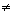 0:
0: 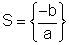
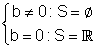
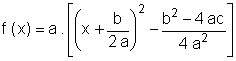
 = b2 - 4 ac;
= b2 - 4 ac; 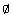
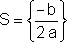
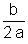 , diz-se raiz dupla da equação.
, diz-se raiz dupla da equação.