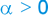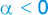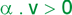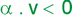Movimento Uniformemente Variado
- Home
- Movimento Uniformemente Variado
Movimento Uniformemente Variado - Movimentos Acelerado e Retardado
Dizemos que um movimento é uniformemente variado quando a aceleração escalar é constante e diferente de zero.
![]()
Equação do Movimento Uniformemente Variado (M.U.V.)
Consideremos uma partícula em M.U.V. de aceleração escalar α. No instante t = 0 a partícula tem espaço so (espaço inicial) e velocidade escalar vo (velocidade inicial). Num instante posterior t qualquer a partícula tem espaço s e velocidade escalar v.
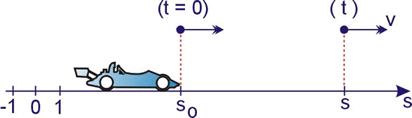
Como a aceleração escalar é constante temos:
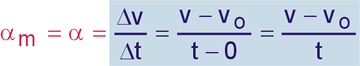 ou
ou 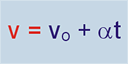
Esta última equação é chamada de equação horária da velocidade escalar do M.U.V.
Para obter a equação horária do espaço é necessário aplicar a teoria das derivadas e integrais, que não faz parte do programa do vestibular. Assim vamos apresentar essa equação sem demonstração:
![]()
As equações anteriores são suficientes para resolver qualquer problema de M.U.V. No entanto, em certos casos, o problema é resolvido mais rapidamente usando uma equação, conhecida pelo nome de “Equação de Torricelli”, que é obtida a partir das equações horárias do espaço e da velocidade escalares.
![]()
Generalizando:
![]()
Propriedade do M.U.V.
Entre dois instantes quaisquer ti e tf, vale a seguinte igualdade:
![]()
Movimentos Acelerado e Retardado
Dizemos que um movimento é acelerado quando o módulo da velocidade escalar aumenta com o tempo. Dizemos que o movimento é retardado quando o módulo da velocidade diminui com o tempo.
movimento acelerado ⇒ |v| aumenta
movimento retardado ⇒ |v| diminui
Analisando os sinais de v e α, concluímos que:
a) Num movimento acelerado, a velocidade escalar (v) e a aceleração escalar (α) têm o mesmo sinal, isto é, ou são ambas positivas ou ambas negativas;
b) Num movimento retardado a velocidade escalar (v) e a aceleração (α) têm sinais contrários:
Resumindo:
|
Acelerado |
Retardado |
|
|
Progressivo |
v > 0 e |
v > 0 e |
|
Retrógrado |
v < 0 e |
v < 0 e |
|
Regra prática |
|
|
Na regra prática se a velocidade e a aceleração têm o mesmo sinal (< ou >), significa que o movimento é acelerado, entretanto se os sinais da velocidade e aceleração são opostos, significa que o movimento é retardado.
Aceleração Escalar
Aceleração Escalar Instantânea (α)
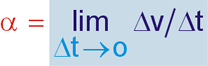
Aceleração Escalar Média (αm)
Consideremos uma partícula que tem velocidade escalares vA e vB nos instantes tA e tB, respectivamente, com tB > tA. Definimos a aceleração média (αm) entre os instantes tA e tB por:
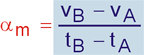
Generalizando
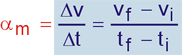
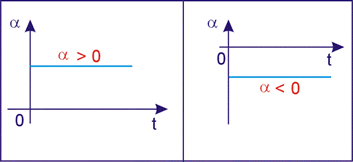
Gráfico da aceleração escalar em função do tempo
Um movimento uniformemente variado possui aceleração escalar constante e diferente de zero. Portanto o gráfico da aceleração escalar em função do tempo é uma reta paralela ao eixo t.
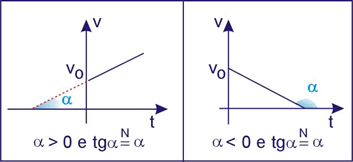
A equação horária da velocidade escalar é
![]()
, isto é, uma equação do primeiro grau em v e t. Portanto, o gráfico da velocidade escalar em função do tempo é retilíneo.
A equação horária do espaço é do segundo grau em t :
![]()
Portanto o gráfico do espaço em função do tempo é parabólico.
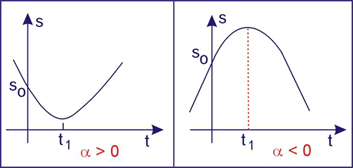
O vértice da parábola corresponde ao instante (t1) em que a velocidade é nula.
PROPRIEDADES DOS GRÁFICOS
Gráfico da velocidade escalar em função do tempo
Dado um gráfico da velocidade escalar em função do tempo, a área da figura situada entre o gráfico e o eixo dos tempos, é numericamente igual à variação de espaço (Δs).
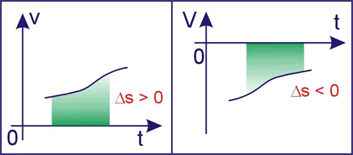
Gráfico da aceleração escalar em função do tempo
Dado um gráfico da aceleração escalar em função do tempo, a área da figura entre o gráfico e o eixo dos tempos, é numericamente igual à variação de velocidade escalar (Δv).
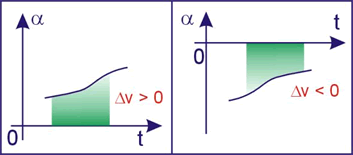
Sumário
- Movimento Uniformemente Variado
i. Equação do Movimento Uniformemente Variado
ii. Propriedade do Movimento Uniformemente Variado
iii. Movimentos Acelerado e Retardado
- Aceleração Escalar
i. Aceleração Escalar Instantânea
ii Aceleração Escalar Média
- Gráfico da aceleração escalar em função do tempo
- Propriedades dos Gráficos
i. Gráfico da velocidade escalar em função do tempo
ii. Gráfico da aceleração escalar em função do tempo
Áreas exclusivas para assinantes